Last updated: 2025-07-29

Checks: 7 0

Knit directory: SCHEDULING/

This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20221107)

The command set.seed(20221107) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: dfde601

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version dfde601. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/patch_selection.png
    Ignored:    analysis/patch_selection_8.png
    Ignored:    analysis/patch_selection_avg.png
    Ignored:    analysis/site_libs/

Untracked files:
    Untracked:  analysis/Notes.txt
    Untracked:  analysis/additional_scripts.R
    Untracked:  analysis/analysis_2025_deadlines.Rmd
    Untracked:  analysis/analysis_2025_dynamicNoise_fixed.Rmd
    Untracked:  analysis/analysis_exp10_preemption.Rmd
    Untracked:  analysis/analysis_exp10_preemption1and2.Rmd
    Untracked:  analysis/analysis_exp10b_preemption-pareto.Rmd
    Untracked:  analysis/analysis_exp11_facesInNoise.Rmd
    Untracked:  analysis/analysis_exp11_facesInNoise_EW.Rmd
    Untracked:  analysis/analysis_exp11_facesInNoise_EW_v2.Rmd
    Untracked:  analysis/analysis_exp12_variability.Rmd
    Untracked:  analysis/analysis_exp12_variability_cynthia.Rmd
    Untracked:  analysis/analysis_exp12_variability_cynthia_update.Rmd
    Untracked:  analysis/analysis_exp13_preemption.Rmd
    Untracked:  analysis/analysis_exp14_ASD_individual_differences.Rmd
    Untracked:  analysis/analysis_exp3a_rdk_dynamic_delay - Copy.Rmd
    Untracked:  analysis/analysis_exp9_preselection.Rmd
    Untracked:  analysis/analysis_exp9_preselection1and2.Rmd
    Untracked:  analysis/analysis_exp9_select-then-complete.Rmd
    Untracked:  analysis/anovaData/
    Untracked:  analysis/archive/
    Untracked:  analysis/correlation_test.m
    Untracked:  analysis/fd_pl.rds
    Untracked:  analysis/fu_pl.rds
    Untracked:  analysis/instructions_for_honours_students.txt
    Untracked:  analysis/joyPlot.m
    Untracked:  analysis/joyPlot.zip
    Untracked:  analysis/joyPlot/
    Untracked:  analysis/loadData.m
    Untracked:  analysis/mstrfind.m
    Untracked:  analysis/plotDistanceByTrials.m
    Untracked:  analysis/prereg/
    Untracked:  analysis/reward rate analysis.docx
    Untracked:  analysis/rewardRate.jpg
    Untracked:  analysis/scheduling_analysis_functions.R
    Untracked:  analysis/temp/
    Untracked:  analysis/toAnalyse/
    Untracked:  analysis/wflow_code_string.txt
    Untracked:  code/AUTSIMQ/
    Untracked:  code/DYNAMICNOISE/
    Untracked:  code/FACESINNOISE/
    Untracked:  code/Notes on how the scheduling jsPsych code works.txt
    Untracked:  code/PREEMPT/
    Untracked:  code/PREPLAN/
    Untracked:  code/SCHEDULEPIX/
    Untracked:  code/SCHEDULEPIX_UON/
    Untracked:  code/SCHEDULERDK/
    Untracked:  code/SCHEDULERDK_UON/
    Untracked:  code/SCHEDULE_REWARD/
    Untracked:  code/SCHEDULE_TYPING/
    Untracked:  code/SMALL_N_LETTERNOISE/
    Untracked:  code/TRAIN_PREEMPT/
    Untracked:  code/TRAIN_VARYING_DEADLINES/
    Untracked:  code/autism_quotient.txt
    Untracked:  data/2020_exp1_rdk_data.csv
    Untracked:  data/2020_exp2_rdk_data.csv
    Untracked:  data/2023-exp10-preemption-pareto.csv
    Untracked:  data/2023-exp10-preemption-selections.csv
    Untracked:  data/2023-exp10-preemption.csv
    Untracked:  data/2023-exp11-facesInNoise-unlabelledCondition.csv
    Untracked:  data/2023-exp11-facesInNoise.csv
    Untracked:  data/2023-exp9-preplan.csv
    Untracked:  data/2023-exp9-select-then-complete.csv
    Untracked:  data/2023_AQdata.csv
    Untracked:  data/2024-exp12-variability.csv
    Untracked:  data/2024-exp12-variability_v2.csv
    Untracked:  data/2024-exp12-variability_v3.csv
    Untracked:  data/2024-exp13-preemption.csv
    Untracked:  data/2024-exp13-preemption_v2.csv
    Untracked:  data/2024-scheduling-data.csv
    Untracked:  data/2024_data_rdk_select_first_AQcorrelation_update.csv
    Untracked:  data/2024_data_typing_train_variability.csv
    Untracked:  data/2025_data_dynamic_noise_fixed_locations.csv
    Untracked:  data/2025_data_typing_train_deadlines_exp1rates.csv
    Untracked:  data/2025_data_typing_train_variability_fulldataset.csv
    Untracked:  data/ASRSscoring.csv
    Untracked:  data/OLIFEscoring.csv
    Untracked:  data/OLIFEscoring_v0.csv
    Untracked:  data/POLYscoring.csv
    Untracked:  data/SQL query.txt
    Untracked:  data/archive/
    Untracked:  data/create_database.sql
    Untracked:  data/dataToAnalyse/
    Untracked:  data/data_dictionary_deadlines.csv
    Untracked:  data/data_dictionary_dynamic_noise.csv
    Untracked:  data/data_dictionary_facesInNoise.csv
    Untracked:  data/data_dictionary_preemption.csv
    Untracked:  data/data_dictionary_preplan.csv
    Untracked:  data/data_dictionary_select_then_complete.csv
    Untracked:  data/data_dictionary_variability.csv
    Untracked:  data/exp1_rdk_data_selections.csv
    Untracked:  data/exp2_rdk_data_selections.csv
    Untracked:  data/exp3a_rdk_data_dynamic_selections.csv
    Untracked:  data/exp3b_rdk_data_dynamic_highlight_selections.csv
    Untracked:  data/exp6a_typing_exponential.xlsx
    Untracked:  data/exp6b_typing_linear.xlsx
    Untracked:  data/exp8a_typing_no_reward_data_selections.csv
    Untracked:  data/rawdata_incEmails/
    Untracked:  data/selections/
    Untracked:  data/sona data/
    Untracked:  data/summaryFiles/
    Untracked:  data/temp_AQcorrelationReplication/
    Untracked:  spatial_pdist.Rdata

Unstaged changes:
    Modified:   analysis/analysis_exp2a_labelled_delay.Rmd
    Modified:   analysis/analysis_exp3a_rdk_dynamic_delay.Rmd
    Modified:   analysis/analysis_exp3b_rdk_dynamic_delay_highlight.Rmd
    Modified:   analysis/analysis_exp7e_rdk_reward_points.Rmd
    Modified:   analysis/analysis_exp8a_typing_no_reward.Rmd
    Deleted:    analysis/prereg.Rmd
    Deleted:    analysis/prereg_v2.Rmd
    Deleted:    analysis/prereg_v3.Rmd
    Deleted:    analysis/prereg_v6_AQcorrelation.Rmd
    Modified:   data/README.md
    Modified:   data/data_dictionary.csv
    Modified:   data/data_dictionary_ruby.csv
    Deleted:    data/exp1_rdk_data.csv
    Deleted:    data/exp2_rdk_data.csv

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/analysis_exp1_labelled_nodelay.Rmd) and HTML (docs/analysis_exp1_labelled_nodelay.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	dfde601	knowlabUnimelb	2025-07-29	Update analysis code to use shared file repo
html	2e6ecdf	knowlabUnimelb	2022-11-09	Build site.
Rmd	67e1aac	knowlabUnimelb	2022-11-09	Publish data and analysis files

Daniel R. Little¹, Ami Eidels², and Deborah J. Lin¹

¹ The University of Melbourne, ² The University of Newcastle

Method

Participants

We tested 99 participants (67 F, 30 M, 2 Undeclared). Participants were recruited through the Melbourne School of Psychological Sciences Research Experience Pool (Mean age = 19.4583333, range = 17 - 49). Participants were reimbursed with credit toward completion of a first-year psychology subject.

Forty-nine were assigned to the Fixed Difficulty condition. In this condition, the location of easy, medium, hard, and very hard random dot kinematograms (RDK’s) was held constant across trials.

Fifty were assigned to the Random Difficulty condition. In this condition, the location of easy, medium, hard, and very hard random dot kinematograms (RDK’s) were randomized from trial to trial.

The Fixed Difficulty experiment was completed before the Random Difficulty experiment. Participants only completed one of these.

Design

In each condition, participants completed multiple trials in which they selected and completed RDK tasks. On each trial, participants were shown a set of four RDKs labelled “Easy”, “Medium”, “Hard”, and “Very Hard”. The labels corresponded to the coherence of the RDK; that is, the proportion of dots moving in a coherent direction, which was set to 80%, 50%, 20%, and 0% for the Easy, Medium, Hard, and Very Hard locations, respectively. From the set of four RDKs, participants selected and completed one RDK at a time in any order. The goal of each trial was to complete as many as possible before a deadline. If an incorrect RDK response was made, that RDK was restarted at the same coherence but with a new randomly sampled direction, and the participant had to respond to the RDK again. A new task could not be selected until the RDK was completed successfully.

Version	Author	Date
2e6ecdf	knowlabUnimelb	2022-11-09

Participants first completed 10 trials with a long (30 sec) deadline to help participants learn the task, explore strategies, and allow for comparison to a short-deadline condition. We term this the no deadline condition since the provided time is well beyond what is necessary to complete all four RDK’s. Next, participants completed 30 trials with a 6 second deadline.

Data Cleaning

Subjects completed the experiment by clicking a link with the uniquely generated id code. Subjects were able to use the link multiple times; further, subjects were able to exit the experiment at any time. Consequently, the datafile contains partially completed data for some subjects which needed to be identified and removed.

After removing any participants who had less than chance accuracy on the easiest RDK indicating equipment problems or a misunderstanding of task directions, there were 42 and 42 in the fixed and random location conditions, respectively.

Average number of correctly completed tasks in each condition
condition	phase	mean	sd
fixed_location	untimed	3.91	0.40
fixed_location	deadline	3.39	0.85
random_location	untimed	3.86	0.51
random_location	deadline	3.21	0.86

REPEATED MEASURES ANOVA

Within Subjects Effects
─────────────────────────────────────────────────────────────────────────────────────────────────── Sum of Squares df Mean Square F p η²-p
─────────────────────────────────────────────────────────────────────────────────────────────────── Phase 14.6946740 1 14.6946740 131.174765 < .0000001 0.6182392
Phase:condition 0.1384581 1 0.1384581 1.235973 0.2695376 0.0150296
Residual 9.0739144 81 0.1120236
─────────────────────────────────────────────────────────────────────────────────────────────────── Note. Type 3 Sums of Squares

Between Subjects Effects
────────────────────────────────────────────────────────────────────────────────────────── Sum of Squares df Mean Square F p η²-p
────────────────────────────────────────────────────────────────────────────────────────── condition 0.4076075 1 0.4076075 1.413901 0.2378841 0.0171561
Residual 23.3511513 81 0.2882858
────────────────────────────────────────────────────────────────────────────────────────── Note. Type 3 Sums of Squares

ASSUMPTIONS

Tests of Sphericity
──────────────────────────────────────────────────────────────────────────────── Mauchly’s W p Greenhouse-Geisser ε Huynh-Feldt ε
──────────────────────────────────────────────────────────────────────────────── Phase 1.000000 NaN ᵃ 1.000000 1.000000
──────────────────────────────────────────────────────────────────────────────── ᵃ The repeated measures has only two levels. The assumption of sphericity is always met when the repeated measures has only two levels

Homogeneity of Variances Test (Levene’s)
────────────────────────────────────────────────────── F df1 df2 p
────────────────────────────────────────────────────── untimed 0.859189239 1 81 0.3567194
deadline 0.005623922 1 81 0.9404053
──────────────────────────────────────────────────────

Data Analysis

We first summarize performance by answering the following questions:

Task completions

How many tasks are completed on average?

Across both conditions, participants completed 3.88 tasks during the untimed phase and 3.3 tasks during the deadline phase.

As one might expect, there were fewer tasks completed under a deadline than without a deadline. There was no difference between conditions and no interaction between deadline and location condition.

RDK performance

We next analysed performance on the RDK discriminations. We then asked:

What was the average completion time and accuracy of the easy, medium, hard, and very hard tasks?

RTs became shorter and more accurate as the difficulty of the RDK became easier. As expected, the RTs were shorter under a deadline than without a deadline. We visualised the response times in two ways: First, we simply took the average of each attempt on each RDK.

Version	Author	Date
2e6ecdf	knowlabUnimelb	2022-11-09

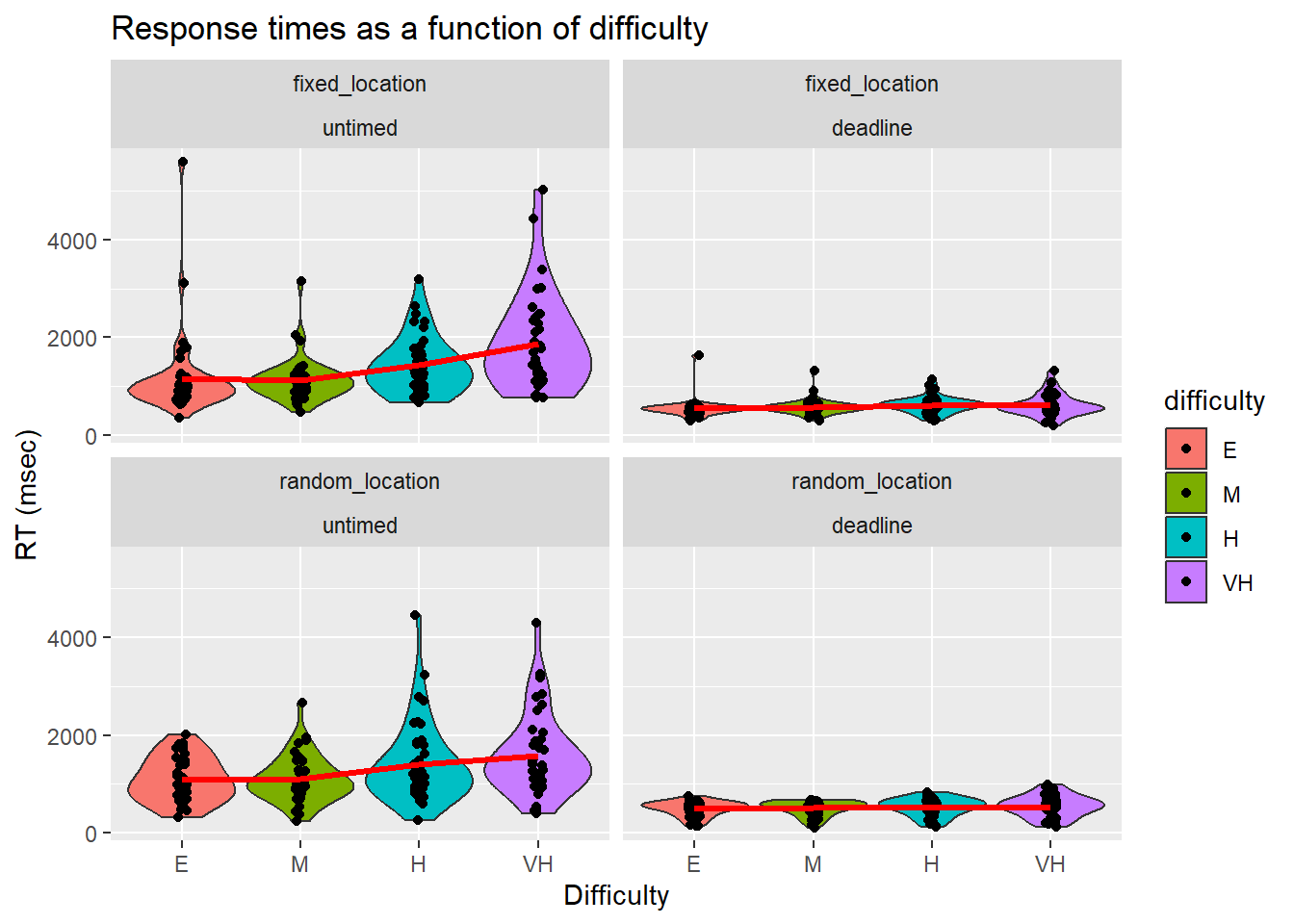
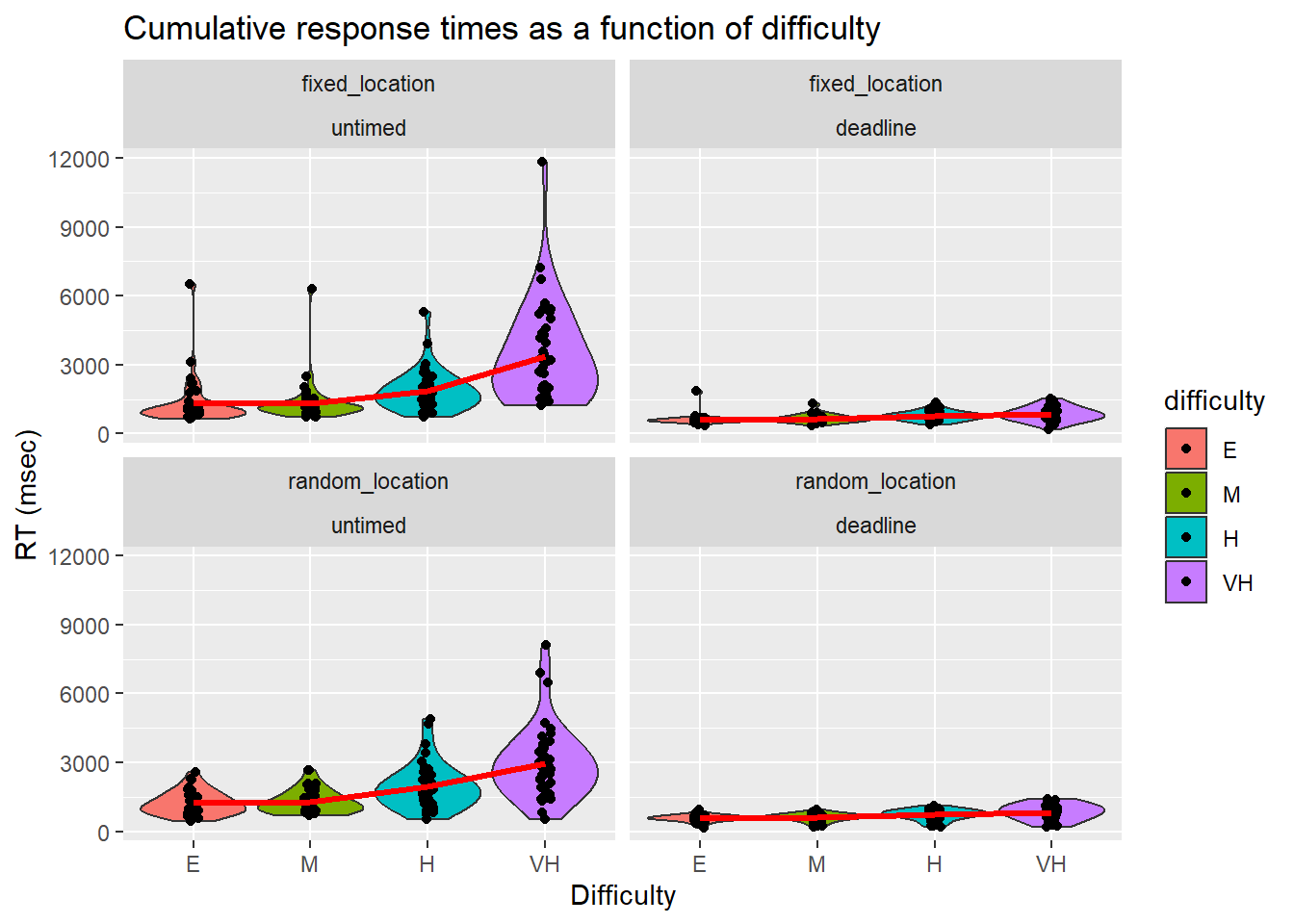
Second, we computed the time to complete an RDK as the cumulative sum across multiple attempts within a trial (termed Cumulative RT or cRT). That is, if an error is made and the RDK needs to be repeated, then the total RT is the sum of both attempts.

We further broke down RTs by condition, deadline, and difficulty.

Mean accuracy, RT, summed RT, and reward rate attempts for each difficulty and each phase
condition	phase	difficulty	acc	se_acc	rt	se_rt	crt	se_crt	rr	se_rr
fixed_location	untimed	easy	0.91	0.02	1158.72	131.54	1302.32	154.89	0.89	0.06
fixed_location	untimed	medium	0.90	0.02	1130.91	69.39	1319.16	136.24	0.81	0.04
fixed_location	untimed	hard	0.80	0.03	1430.60	89.39	1860.39	134.97	0.52	0.04
fixed_location	untimed	v. hard	0.59	0.03	1869.86	147.80	3382.98	327.23	0.25	0.03
fixed_location	deadline	easy	0.90	0.02	543.88	30.18	606.52	33.42	1.58	0.07
fixed_location	deadline	medium	0.88	0.02	571.78	25.37	647.44	26.47	1.46	0.07
fixed_location	deadline	hard	0.75	0.03	619.82	26.87	766.76	32.01	1.07	0.07
fixed_location	deadline	v. hard	0.63	0.03	609.25	36.47	845.66	49.36	0.92	0.09
random_location	untimed	easy	0.89	0.02	1090.37	67.09	1226.66	75.64	0.85	0.06
random_location	untimed	medium	0.85	0.03	1100.27	71.56	1294.34	76.49	0.74	0.05
random_location	untimed	hard	0.73	0.02	1410.00	122.79	1948.14	148.66	0.47	0.04
random_location	untimed	v. hard	0.54	0.02	1580.82	126.33	2954.52	239.09	0.26	0.04
random_location	deadline	easy	0.85	0.02	489.72	23.02	567.61	22.25	1.65	0.13
random_location	deadline	medium	0.82	0.02	507.94	23.16	607.93	25.87	1.50	0.10
random_location	deadline	hard	0.67	0.02	523.48	27.56	720.06	34.89	1.11	0.11
random_location	deadline	v. hard	0.58	0.02	543.81	33.77	837.53	52.85	0.98	0.14

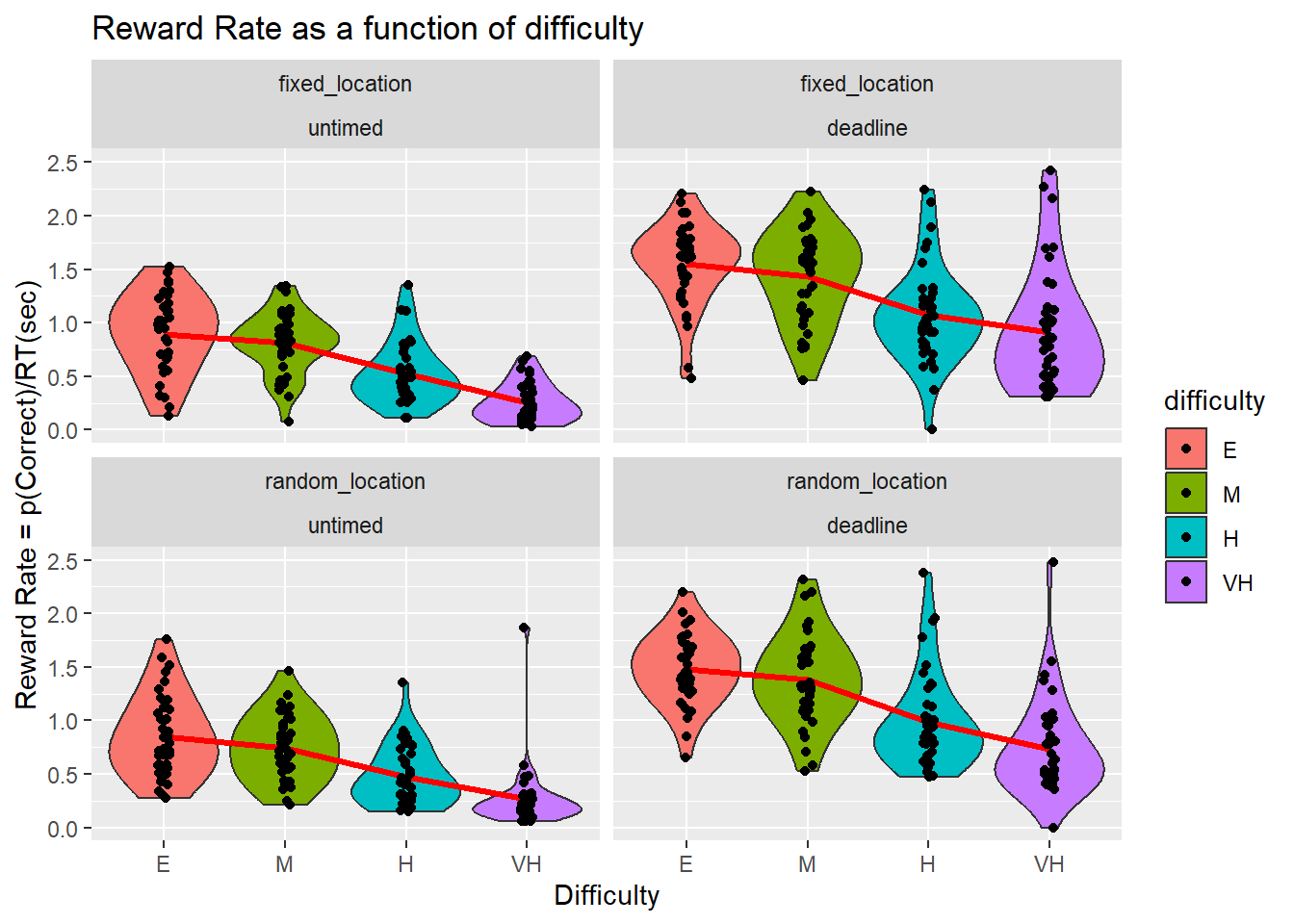
Reward Rate

To confirm that coherence offered a good proxy for difficulty (and hence, that an optimal order of easiest to hardest was maintained), we calculated the reward rate for each patch. Reward rate can be defined as “the proportion of correct trials divided by the average duration between decisions” (Gold & Shadlen, 2002), and is tantamount, in our task, to percentage of correct responses per unit time (Bogacz et al, 2006). For our purposes, we can fix time at 1 sec calculate the Reward Rate as the number of RDK tasks completed in 1 sec.

Inspection of the figure reveals that RR is roughly monotonically increasing when tasks become easier. Under such conditions, the optimal order of task-completion should be easy-to-hardest. This could change in a predictable manner if people value differently easy and hard tasks (overweight completion of harder tasks). The only notable exception was in the fixed, no deadline task, where the easy and medium RDK conditions had equal RR.

	name[none]	ss[none]	df[none]	ms[none]	F[none]	p[none]	partEta[none]
“Phase”	Phase	75.311	1	75.311	142.298	0.000	0.643
[“Phase”,“condition”]	Phase:condition	0.345	1	0.345	0.653	0.422	0.008
[“Phase”,“condition”,“.RES”]	Residual	41.811	79	0.529	NA	NA	NA
“Difficulty”	Difficulty	42.515	3	14.172	109.161	0.000	0.580
[“Difficulty”,“condition”]	Difficulty:condition	0.101	3	0.034	0.260	0.854	0.003
[“Difficulty”,“condition”,“.RES”]	Residual	30.768	237	0.130	NA	NA	NA
[“Phase”,“Difficulty”]	Phase:Difficulty	0.371	3	0.124	1.160	0.326	0.014
[“Phase”,“Difficulty”,“condition”]	Phase:Difficulty:condition	0.038	3	0.013	0.118	0.950	0.001
[“Phase”,“Difficulty”,“condition”,“.RES”]	Residual	25.304	237	0.107	NA	NA	NA

	name	ss	df	ms	F	p	partEta
“condition”	condition	0.000	1	0.000	0	0.993	0
“Residual”	Residual	59.085	79	0.748	NA	NA	NA

Optimality in each condition

Having now established that the RDK’s are ordered in accuracy, difficulty, and reward rate, it is clear that the task set presented to each subject has an optimal solution, ordered from easiest to most difficult. We now ask:

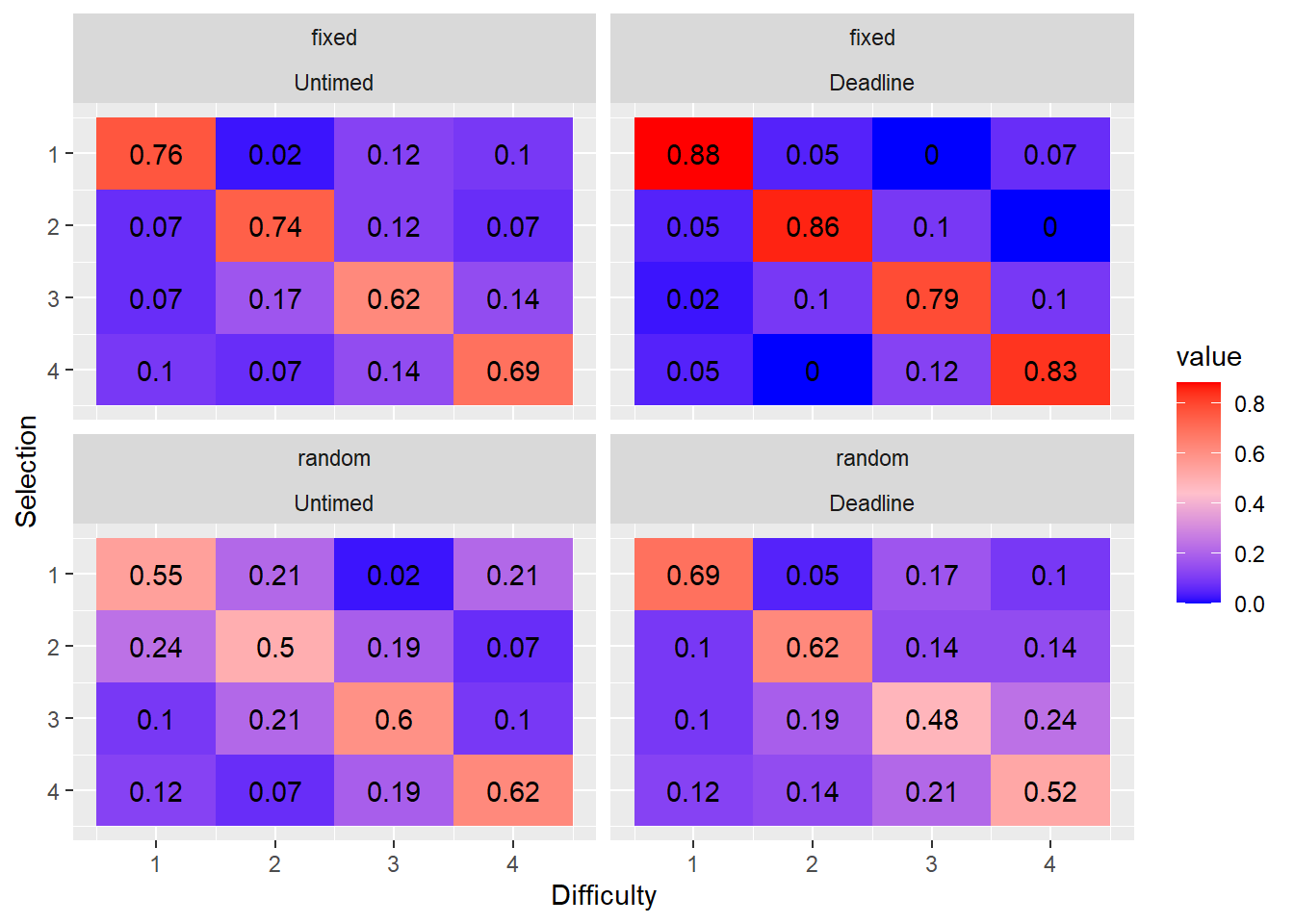
What is the proportion of easy, medium, hard, and very hard tasks selected first, second, third or fourth?

We first compute the marginal distribution of the ranks of each of the tasks; in other words, what are the proportions of the ranks of each task in each rank position. These matrices indicate the proportions of responses for each difficulty level which were chosen first, second, third, or fourth, respectively. The matrix from a dataset in which choice is always optimal would have ones on the diagonal and zeros on the off-diagonal.

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) [glmerMod] Family: poisson ( log ) Formula: value ~ condition + phase + Difficulty + Order + condition:phase +
(1 | subject) Data: df

 AIC      BIC   logLik deviance df.resid

23324.5 23389.1 -11651.2 23302.5 2613

Scaled residuals: Min 1Q Median 3Q Max -2.7076 -1.5836 -0.8213 0.7660 8.3725

Random effects: Groups Name Variance Std.Dev. subject (Intercept) 0.008926 0.09448 Number of obs: 2624, groups: subject, 83

Fixed effects: Estimate Std. Error z value Pr(>|z|) (Intercept) 8.964e-01 2.895e-02 30.964 <2e-16 conditionrandom_location -1.483e-02 4.079e-02 -0.363 0.716 phasedeadline 1.073e+00 2.915e-02 36.798 <2e-16 Difficulty.L 2.929e-06 1.804e-02 0.000 1.000 Difficulty.Q -7.897e-07 1.804e-02 0.000 1.000 Difficulty.C 8.563e-08 1.804e-02 0.000 1.000 Order.L -1.736e-07 1.804e-02 0.000 1.000 Order.Q -6.680e-07 1.804e-02 0.000 1.000 Order.C -1.143e-06 1.804e-02 0.000 1.000 conditionrandom_location:phasedeadline -4.957e-02 4.101e-02 -1.209 0.227

(Intercept) conditionrandom_location
phasedeadline Difficulty.L
Difficulty.Q
Difficulty.C
Order.L
Order.Q
Order.C
conditionrandom_location:phasedeadline
— Signif. codes: 0 ‘’ 0.001 ’’ 0.01 ’’ 0.05 ‘.’ 0.1 ’ ’ 1

Correlation of Fixed Effects: (Intr) cndtn_ phsddl Dffc.L Dffc.Q Dffc.C Ordr.L Ordr.Q Ordr.C cndtnrndm_l -0.709
phasedeadln -0.733 0.521
Difficlty.L 0.000 0.000 0.000
Difficlty.Q 0.000 0.000 0.000 0.000
Difficlty.C 0.000 0.000 0.000 0.000 0.000
Order.L 0.000 0.000 0.000 0.000 0.000 0.000
Order.Q 0.000 0.000 0.000 0.000 0.000 0.000 0.000
Order.C 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
cndtnrndm_: 0.521 -0.736 -0.711 0.000 0.000 0.000 0.000 0.000 0.000

Do the marginal distributions differ from uniformity?

We tested whether the marginal distributions were different from uniformally random selection using the fact that the mean rank is distributed according to a \(\chi^2\) distribution with the following test-statistic: \[\chi^2 = \frac{12N}{k(k+1)}\sum_{j=1}^k \left(m_j - \frac{k+1}{2} \right)^2\] see (Marden, 1995).

    condition    phase  chi2 df p

1 fixed_location untimed 50.14 3 0 2 fixed_location deadline 87.91 3 0 3 random_location untimed 30.89 3 0 4 random_location deadline 32.09 3 0

It is evident at a glance that the ordering of choices is more optimal when the locations are fixed; that is, the proportions on the diagonal are higher. When the locations are fixed, choice order becomes more optimal under a deadline. By contrast, when locations are random, responding becomes less optimal under a deadline. This likely reflects the additional costs of having to search for the appropriate task to complete. This search is minimised in the fixed location condition.

How optimal were responses?

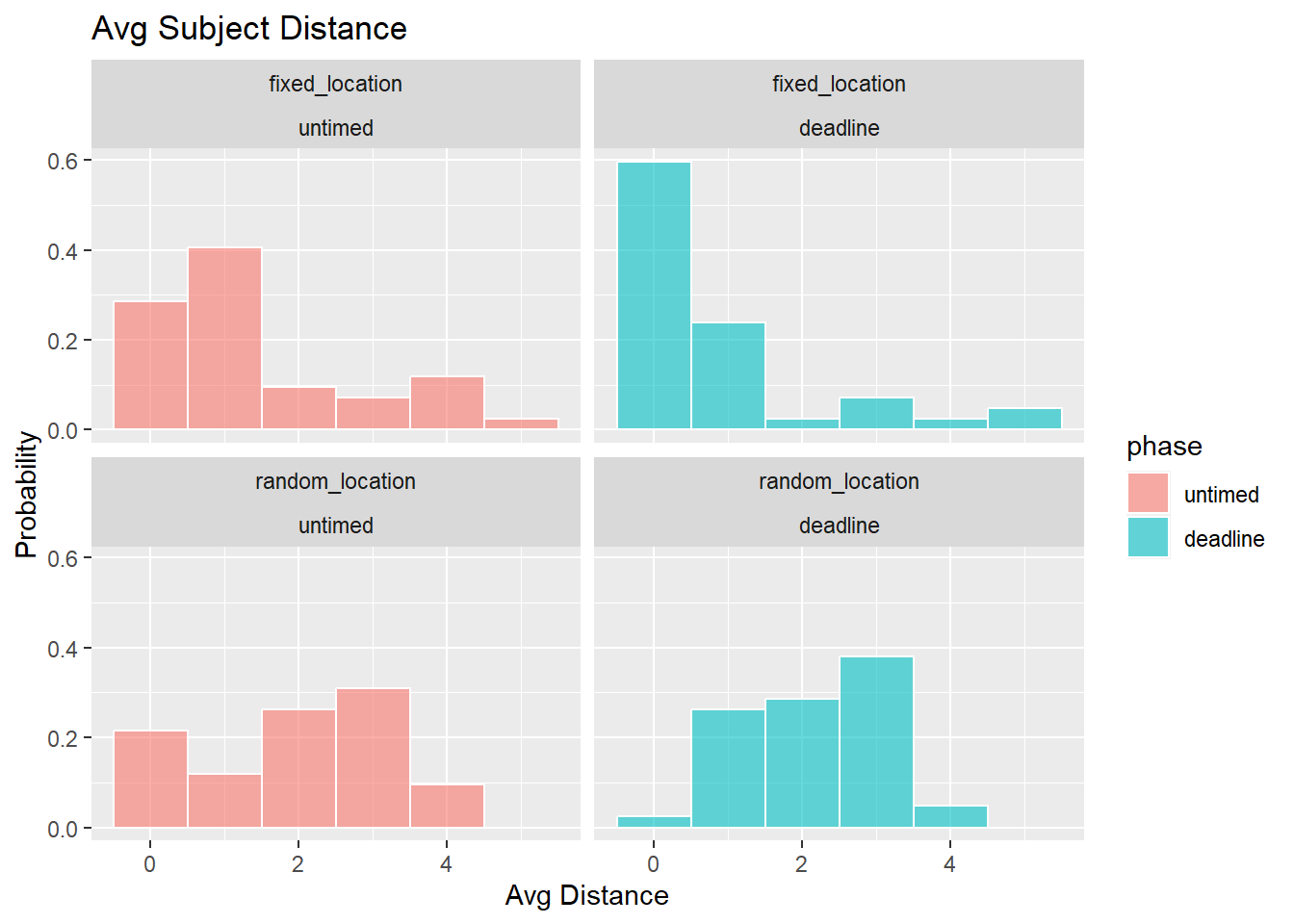
The next analysis computed the distance between the selected order and the optimal order (easiest to very hard for that trial), which ranges between 0 (perfect match) and 6 (maximally distant), for 4 options.

What we want is the distance of the selected options from the optimal solutions, which is the edit distance (or number of discordant pairs) between orders. However, because a participant may run out of time, there may be missing values. To handle these values, for each trial, we find the orders which partially match the selected order and compute three the average distance of those possible orders and the optimal solution (avg_distance).

The following figure compares the avg_distance between the fixed difficulty and random difficulty conditions as a function of deadline condition and phase. For each of these measures, lower values reflect respones which are closer to optimal.

Stability of selections

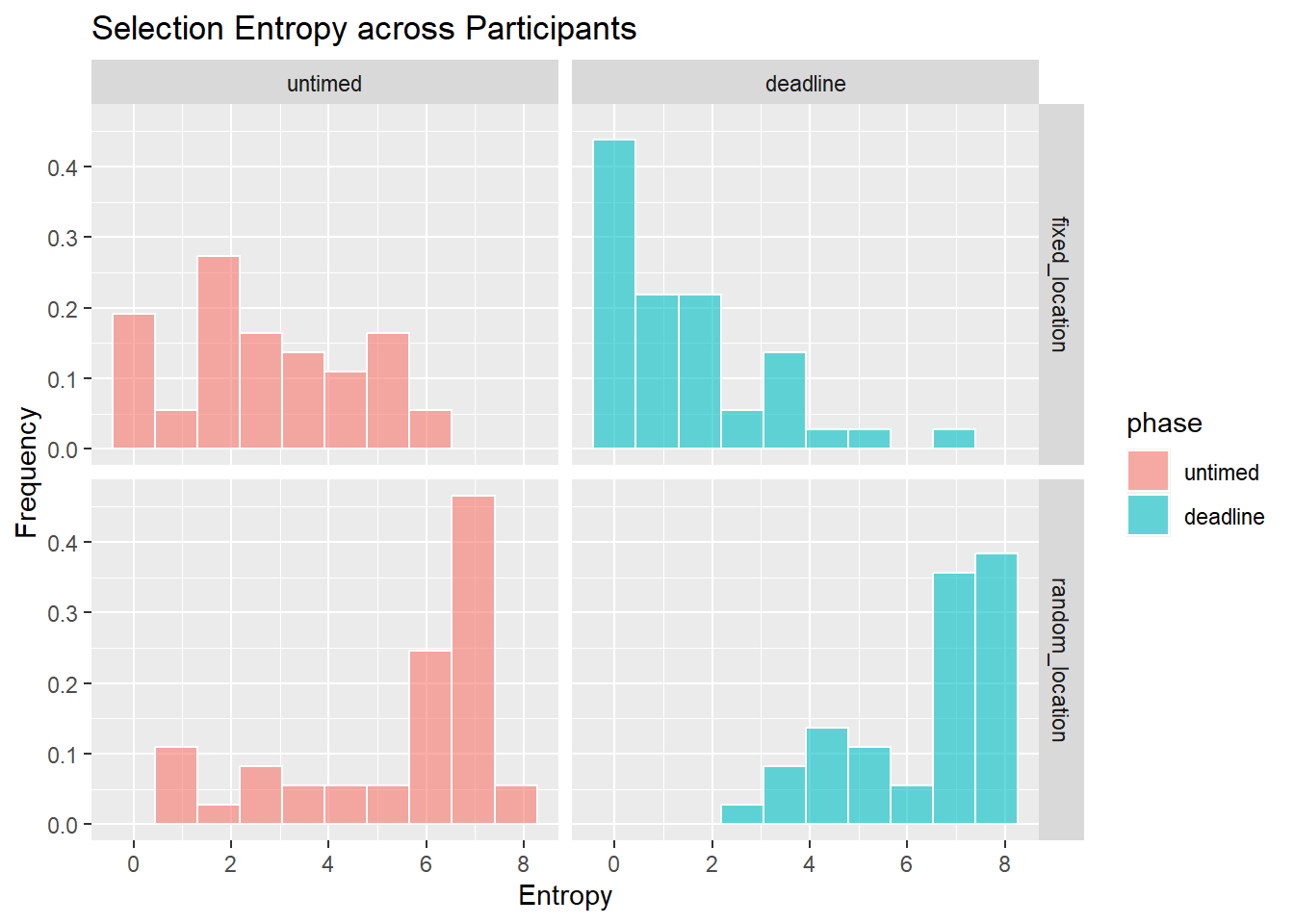
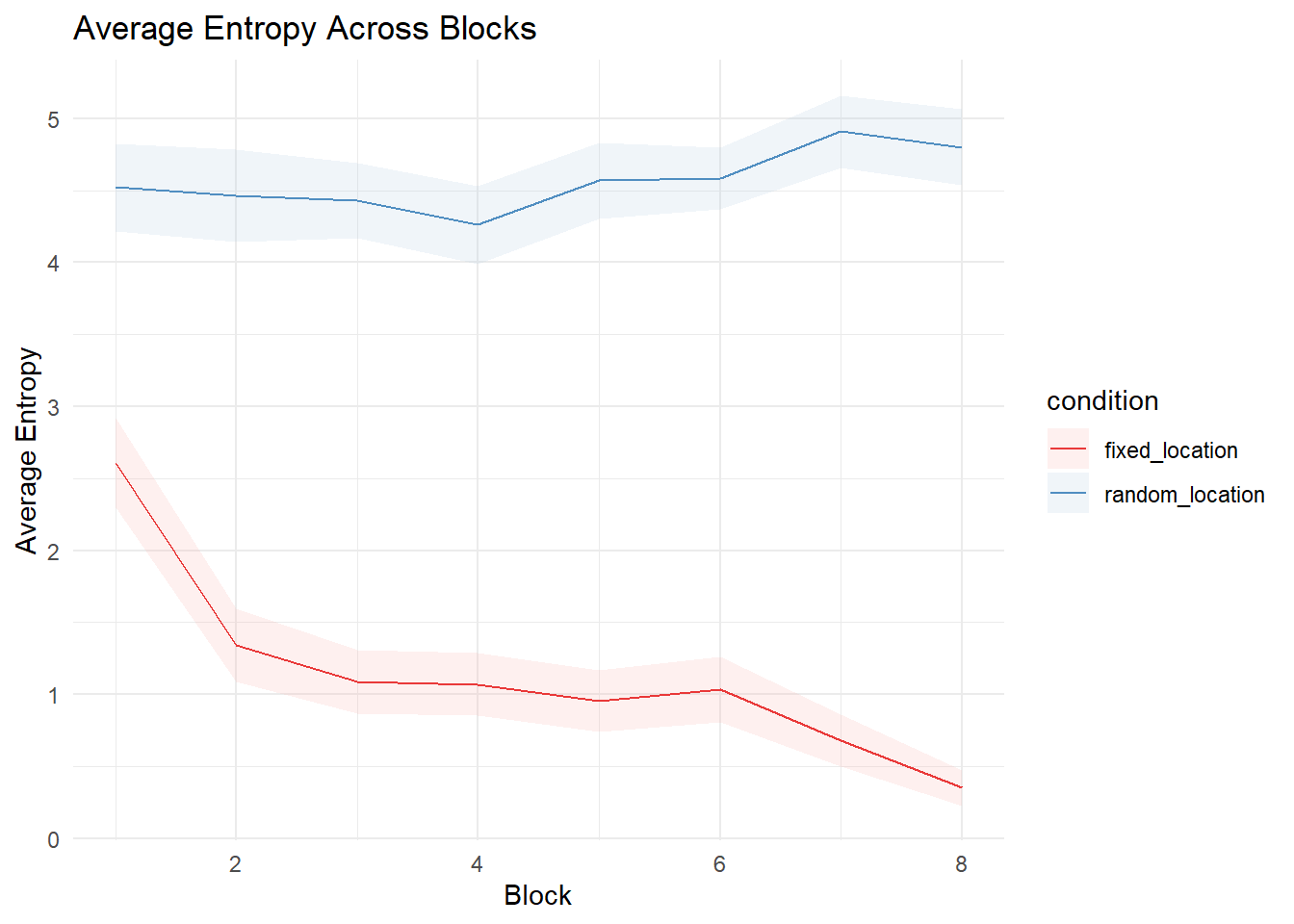
Selection Choice RTs

Mean RTs for each scheduling selection
condition	phase	mrt_sel1	mrt_sel2	mrt_sel3	mrt_sel4
fixed_location	deadline	733.74	697.44	673.00	638.96
fixed_location	untimed	1520.91	1318.98	1053.88	966.72
random_location	deadline	946.69	808.86	717.85	637.53
random_location	untimed	1853.18	1461.47	1238.13	1044.61

REPEATED MEASURES ANOVA

Within Subjects Effects
─────────────────────────────────────────────────────────────────────────────────────────────────────────────── Sum of Squares df Mean Square F p η²-p
─────────────────────────────────────────────────────────────────────────────────────────────────────────────── Phase 4.664583e+7 1 4.664583e+7 255.9082108 < .0000001 0.7687050
Phase:condition 734461.06 1 734461.06 4.0293977 0.0482230 0.0497276
Residual 1.403522e+7 77 182275.65
Selection 1.391609e+7 3 4638697.65 75.9680887 < .0000001 0.4966270
Selection:condition 1647915.45 3 549305.15 8.9959867 0.0000117 0.1046094
Residual 1.410512e+7 231 61061.13
Phase:Selection 6779771.28 3 2259923.76 48.5913034 < .0000001 0.3869002
Phase:Selection:condition 84503.25 3 28167.75 0.6056433 0.6119518 0.0078041
Residual 1.074354e+7 231 46508.81
─────────────────────────────────────────────────────────────────────────────────────────────────────────────── Note. Type 3 Sums of Squares

Between Subjects Effects
────────────────────────────────────────────────────────────────────────────────────────── Sum of Squares df Mean Square F p η²-p
────────────────────────────────────────────────────────────────────────────────────────── condition 5419445 1 5419445.3 9.554512 0.0027764 0.1103872
Residual 4.367542e+7 77 567213.2
────────────────────────────────────────────────────────────────────────────────────────── Note. Type 3 Sums of Squares

ASSUMPTIONS

Tests of Sphericity
─────────────────────────────────────────────────────────────────────────────────────────── Mauchly’s W p Greenhouse-Geisser ε Huynh-Feldt ε
─────────────────────────────────────────────────────────────────────────────────────────── Phase 1.0000000 NaN ᵃ 1.0000000 1.0000000
Selection 0.4496834 < .0000001 0.6473440 0.6638358
Phase:Selection 0.4955847 < .0000001 0.6708009 0.6888580
─────────────────────────────────────────────────────────────────────────────────────────── ᵃ The repeated measures has only two levels. The assumption of sphericity is always met when the repeated measures has only two levels.

Homogeneity of Variances Test (Levene’s)
─────────────────────────────────────────────────────────── F df1 df2 p
─────────────────────────────────────────────────────────── rt1_untimed 3.061421071 1 77 0.0841556
rt2_untimed 0.303103197 1 77 0.5835373
rt3_untimed 4.678451762 1 77 0.0336465
rt4_untimed 0.310075744 1 77 0.5792487
rt1_deadline 16.496449731 1 77 0.0001163
rt2_deadline 0.629107238 1 77 0.4301203
rt3_deadline 0.022738712 1 77 0.8805329
rt4_deadline 0.006947157 1 77 0.9337899
───────────────────────────────────────────────────────────

Selection model

We can treat each task selection as a probabilistic choice given by a Luce’s choice rule (Luce, 1959), where each task is represented by some strength, \(\nu\). The probability of selecting task \(i_j\) from set \(S = \{i_1, i_2, ..., i_J \}\), where J is the number of tasks, is:

\[p\left(i_j |S \right) = \frac{\nu_{i_j}}{\sum_{i \in S} \nu_{i}}. \]

Plackett (1975) generalised this model to explain the distribution over a sequence of choices (i.e., ranks). In this case, after each choice, the choice set is reduce by one (i.e., sampling without replacement). This probability of observing a specific selection order, \(i_1 \succ ... \succ i_J\) is:

\[p\left(i_j |A \right) = \prod_{j=1}^J \frac{\nu_{i_j}}{\sum_{i \in A_j} \nu_{i}}, \]

where \(A_j\) is the current choice set.

Sampling distribution anlaysis

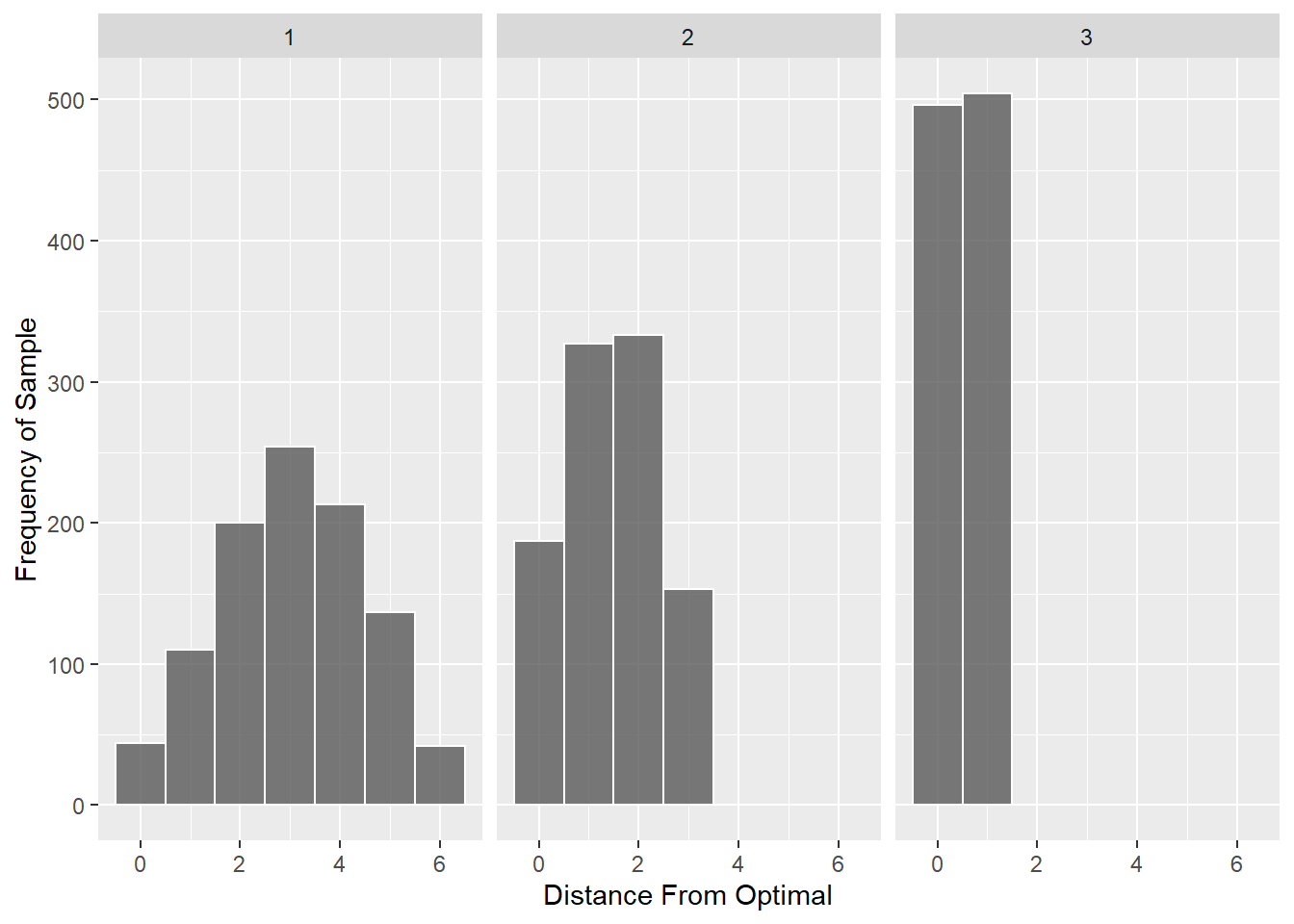
In order to characterise performance, we examined three sampling distributions for comparison to our data. The first is the sampling distribution of edit distances from optimal assuming that orders are sampled uniformly at random. The second distribution assumes that the first choice was optimal but the remaining orders are sampled at random. Finally, the third distributions assumes that the first two choices are selected optimally but that the remaining are randomly selected. It is clear that the mode of the distribution moves from a distance of 3 to a distance of 0 as the sampling distribution summarises orders which better conform to optimality.

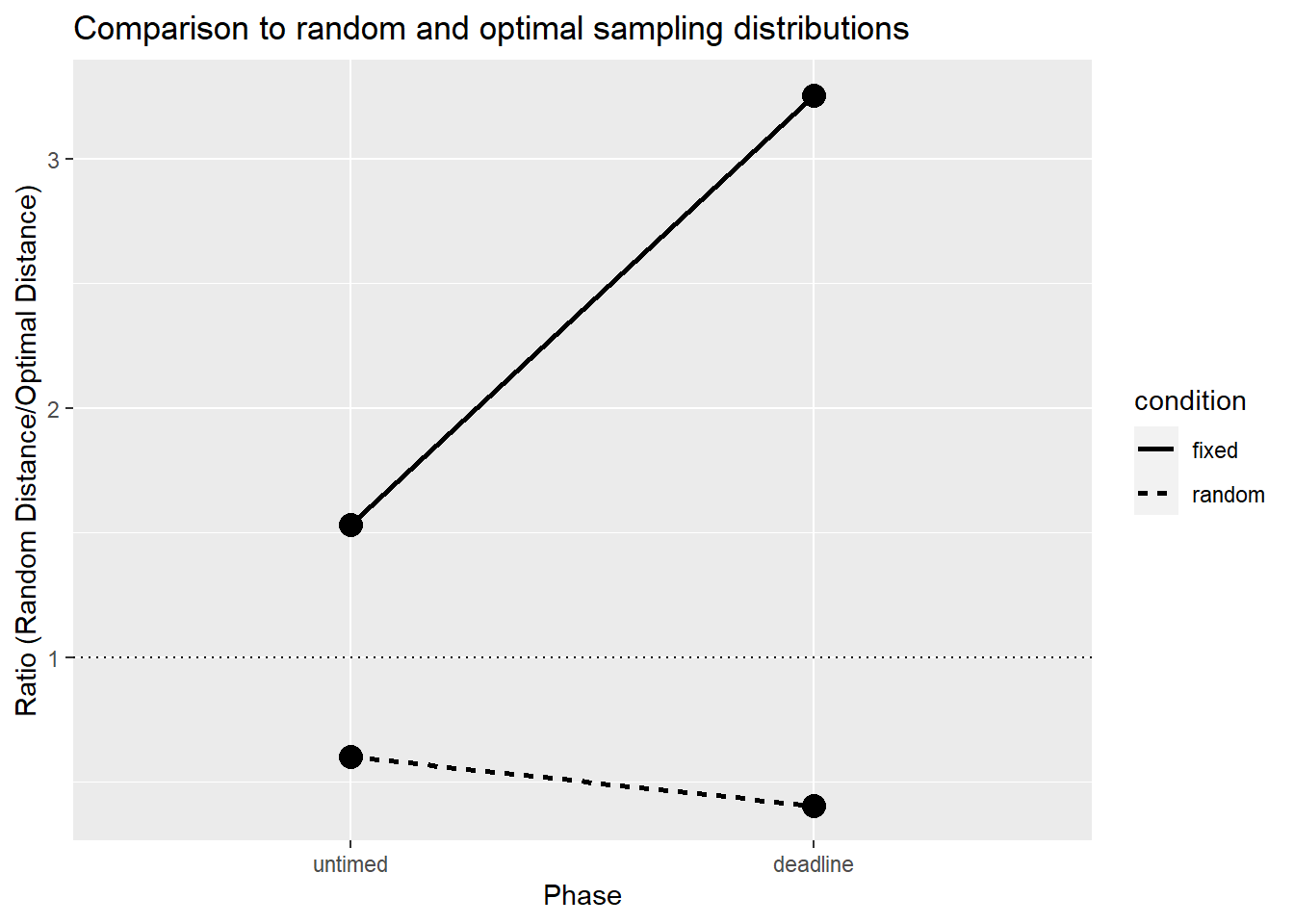
To characterise the optimality of each condition at each point in the experiment, we first computed the ks-test statistic between the data (the average partial distance data) and the random order distribution and the first-two optimal distribution. Since smaller ks-statistics indicate a closer match between the distributions, we then took the ratio of the ks-statistics (random over first two-optimal). Values less than one indicate that the data are more consistent with random than optimal responding. Values greater than one indicate that the data are more consistent with optimal rather than random responding.

Version	Author	Date
2e6ecdf	knowlabUnimelb	2022-11-09

Version	Author	Date
2e6ecdf	knowlabUnimelb	2022-11-09

This figure efficiently summarises the main result: responding is more optimal in the fixed deadline condition particularly under a deadline; in the random deadline conditions, responding was closer to a random sampling distribution than to an optimal sampling distribution.

sessionInfo()

R version 4.3.1 (2023-06-16 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19045)

Matrix products: default


locale:
[1] LC_COLLATE=English_Australia.utf8  LC_CTYPE=English_Australia.utf8   
[3] LC_MONETARY=English_Australia.utf8 LC_NUMERIC=C                      
[5] LC_TIME=English_Australia.utf8    

time zone: Australia/Sydney
tzcode source: internal

attached base packages:
[1] stats4    grid      stats     graphics  grDevices utils     datasets 
[8] methods   base     

other attached packages:
 [1] statmod_1.5.0     betareg_3.2-0     jmv_2.4.9         pmr_1.2.5.1      
 [5] jpeg_0.1-10       rstatix_0.7.2     lmerTest_3.1-3    lme4_1.1-34      
 [9] Matrix_1.6-1.1    png_0.1-8         reshape2_1.4.4    knitr_1.44       
[13] english_1.2-6     gtools_3.9.4      DescTools_0.99.50 lubridate_1.9.3  
[17] forcats_1.0.0     stringr_1.5.0     dplyr_1.1.3       purrr_1.0.2      
[21] readr_2.1.4       tidyr_1.3.0       tibble_3.2.1      ggplot2_3.4.3    
[25] tidyverse_2.0.0   workflowr_1.7.1  

loaded via a namespace (and not attached):
 [1] gld_2.6.6           sandwich_3.0-2      readxl_1.4.3       
 [4] rlang_1.1.1         magrittr_2.0.3      multcomp_1.4-25    
 [7] git2r_0.32.0        e1071_1.7-13        compiler_4.3.1     
[10] flexmix_2.3-19      getPass_0.2-2       callr_3.7.3        
[13] vctrs_0.6.3         pkgconfig_2.0.3     fastmap_1.1.1      
[16] backports_1.4.1     labeling_0.4.3      utf8_1.2.3         
[19] promises_1.2.1      rmarkdown_2.25      tzdb_0.4.0         
[22] ps_1.7.5            nloptr_2.0.3        modeltools_0.2-23  
[25] xfun_0.40           cachem_1.0.8        jsonlite_1.8.7     
[28] later_1.3.1         afex_1.3-0          parallel_4.3.1     
[31] broom_1.0.5         R6_2.5.1            RColorBrewer_1.1-3 
[34] bslib_0.5.1         stringi_1.7.12      car_3.1-2          
[37] boot_1.3-28.1       estimability_1.4.1  lmtest_0.9-40      
[40] jquerylib_0.1.4     cellranger_1.1.0    numDeriv_2016.8-1.1
[43] Rcpp_1.0.11         zoo_1.8-12          base64enc_0.1-3    
[46] nnet_7.3-19         httpuv_1.6.11       splines_4.3.1      
[49] timechange_0.2.0    tidyselect_1.2.0    rstudioapi_0.15.0  
[52] abind_1.4-5         yaml_2.3.7          codetools_0.2-19   
[55] processx_3.8.2      lattice_0.21-8      plyr_1.8.9         
[58] withr_2.5.1         coda_0.19-4         evaluate_0.22      
[61] survival_3.5-5      proxy_0.4-27        pillar_1.9.0       
[64] carData_3.0-5       whisker_0.4.1       generics_0.1.3     
[67] rprojroot_2.0.3     hms_1.1.3           munsell_0.5.0      
[70] scales_1.2.1        rootSolve_1.8.2.4   minqa_1.2.6        
[73] xtable_1.8-4        jmvcore_2.4.7       class_7.3-22       
[76] glue_1.6.2          emmeans_1.8.8       lmom_3.0           
[79] tools_4.3.1         data.table_1.14.8   Exact_3.2          
[82] fs_1.6.3            mvtnorm_1.2-3       colorspace_2.1-0   
[85] nlme_3.1-162        Formula_1.2-5       cli_3.6.1          
[88] fansi_1.0.4         expm_0.999-7        gtable_0.3.4       
[91] sass_0.4.7          digest_0.6.33       TH.data_1.1-2      
[94] farver_2.1.1        htmltools_0.5.6     lifecycle_1.0.3    
[97] httr_1.4.7          MASS_7.3-60

Experiment 1: RDK Direction Judgement, 4 Tasks, No Error Penalty

knowlabUnimelb

2020-10-29