Experiment 2b: RDK Direction Judgement, Average Completion Time Label, 4 Tasks, 500 msec Error Penalty
knowlabUnimelb
2021-08-24
Last updated: 2025-07-29
Checks: 7 0
Knit directory: SCHEDULING/
This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20221107) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 2c1fd06. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: analysis/patch_selection.png
Ignored: analysis/patch_selection_8.png
Ignored: analysis/patch_selection_avg.png
Ignored: analysis/site_libs/
Untracked files:
Untracked: analysis/Notes.txt
Untracked: analysis/additional_scripts.R
Untracked: analysis/analysis_2025_deadlines.Rmd
Untracked: analysis/analysis_2025_dynamicNoise_fixed.Rmd
Untracked: analysis/analysis_exp10_preemption.Rmd
Untracked: analysis/analysis_exp10_preemption1and2.Rmd
Untracked: analysis/analysis_exp10b_preemption-pareto.Rmd
Untracked: analysis/analysis_exp11_facesInNoise.Rmd
Untracked: analysis/analysis_exp11_facesInNoise_EW.Rmd
Untracked: analysis/analysis_exp11_facesInNoise_EW_v2.Rmd
Untracked: analysis/analysis_exp12_variability.Rmd
Untracked: analysis/analysis_exp12_variability_cynthia.Rmd
Untracked: analysis/analysis_exp12_variability_cynthia_update.Rmd
Untracked: analysis/analysis_exp13_preemption.Rmd
Untracked: analysis/analysis_exp14_ASD_individual_differences.Rmd
Untracked: analysis/analysis_exp9_preselection.Rmd
Untracked: analysis/analysis_exp9_preselection1and2.Rmd
Untracked: analysis/analysis_exp9_select-then-complete.Rmd
Untracked: analysis/anovaData/
Untracked: analysis/archive/
Untracked: analysis/correlation_test.m
Untracked: analysis/fd_pl.rds
Untracked: analysis/fu_pl.rds
Untracked: analysis/instructions_for_honours_students.txt
Untracked: analysis/joyPlot.m
Untracked: analysis/joyPlot.zip
Untracked: analysis/joyPlot/
Untracked: analysis/loadData.m
Untracked: analysis/mstrfind.m
Untracked: analysis/plotDistanceByTrials.m
Untracked: analysis/prereg/
Untracked: analysis/reward rate analysis.docx
Untracked: analysis/rewardRate.jpg
Untracked: analysis/scheduling_analysis_functions.R
Untracked: analysis/temp/
Untracked: analysis/toAnalyse/
Untracked: analysis/wflow_code_string.txt
Untracked: code/AUTSIMQ/
Untracked: code/DYNAMICNOISE/
Untracked: code/FACESINNOISE/
Untracked: code/Notes on how the scheduling jsPsych code works.txt
Untracked: code/PREEMPT/
Untracked: code/PREPLAN/
Untracked: code/SCHEDULEPIX/
Untracked: code/SCHEDULEPIX_UON/
Untracked: code/SCHEDULERDK/
Untracked: code/SCHEDULERDK_UON/
Untracked: code/SCHEDULE_REWARD/
Untracked: code/SCHEDULE_TYPING/
Untracked: code/SMALL_N_LETTERNOISE/
Untracked: code/TRAIN_PREEMPT/
Untracked: code/TRAIN_VARYING_DEADLINES/
Untracked: code/autism_quotient.txt
Untracked: data/2020_exp1_rdk_data.csv
Untracked: data/2020_exp2_rdk_data.csv
Untracked: data/2021_exp2b_rdk_data_avgtime.csv
Untracked: data/2023-exp10-preemption-pareto.csv
Untracked: data/2023-exp10-preemption-selections.csv
Untracked: data/2023-exp10-preemption.csv
Untracked: data/2023-exp11-facesInNoise-unlabelledCondition.csv
Untracked: data/2023-exp11-facesInNoise.csv
Untracked: data/2023-exp9-preplan.csv
Untracked: data/2023-exp9-select-then-complete.csv
Untracked: data/2023_AQdata.csv
Untracked: data/2024-exp12-variability.csv
Untracked: data/2024-exp12-variability_v2.csv
Untracked: data/2024-exp12-variability_v3.csv
Untracked: data/2024-exp13-preemption.csv
Untracked: data/2024-exp13-preemption_v2.csv
Untracked: data/2024-scheduling-data.csv
Untracked: data/2024_data_rdk_select_first_AQcorrelation_update.csv
Untracked: data/2024_data_typing_train_variability.csv
Untracked: data/2025_data_dynamic_noise_fixed_locations.csv
Untracked: data/2025_data_typing_train_deadlines_exp1rates.csv
Untracked: data/2025_data_typing_train_variability_fulldataset.csv
Untracked: data/ASRSscoring.csv
Untracked: data/OLIFEscoring.csv
Untracked: data/OLIFEscoring_v0.csv
Untracked: data/POLYscoring.csv
Untracked: data/SQL query.txt
Untracked: data/archive/
Untracked: data/create_database.sql
Untracked: data/dataToAnalyse/
Untracked: data/data_dictionary_deadlines.csv
Untracked: data/data_dictionary_dynamic_noise.csv
Untracked: data/data_dictionary_facesInNoise.csv
Untracked: data/data_dictionary_preemption.csv
Untracked: data/data_dictionary_preplan.csv
Untracked: data/data_dictionary_select_then_complete.csv
Untracked: data/data_dictionary_variability.csv
Untracked: data/exp3a_rdk_data_dynamic_selections.csv
Untracked: data/exp3b_rdk_data_dynamic_highlight_selections.csv
Untracked: data/exp6a_typing_exponential.xlsx
Untracked: data/exp6b_typing_linear.xlsx
Untracked: data/exp8a_typing_no_reward_data_selections.csv
Untracked: data/rawdata_incEmails/
Untracked: data/selections/
Untracked: data/sona data/
Untracked: data/summaryFiles/
Untracked: data/temp_AQcorrelationReplication/
Untracked: spatial_pdist.Rdata
Unstaged changes:
Modified: analysis/analysis_exp1_labelled_nodelay.Rmd
Modified: analysis/analysis_exp3a_rdk_dynamic_delay.Rmd
Modified: analysis/analysis_exp3b_rdk_dynamic_delay_highlight.Rmd
Modified: analysis/analysis_exp7e_rdk_reward_points.Rmd
Modified: analysis/analysis_exp8a_typing_no_reward.Rmd
Deleted: analysis/prereg.Rmd
Deleted: analysis/prereg_v2.Rmd
Deleted: analysis/prereg_v3.Rmd
Deleted: analysis/prereg_v6_AQcorrelation.Rmd
Modified: data/README.md
Modified: data/data_dictionary.csv
Modified: data/data_dictionary_avgTime.csv
Modified: data/data_dictionary_ruby.csv
Deleted: data/exp1_rdk_data.csv
Deleted: data/exp2_rdk_data.csv
Deleted: data/exp2b_rdk_data_avgtime.csv
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown
(analysis/analysis_exp2b_avgTimelabelled_delay.Rmd) and
HTML (docs/analysis_exp2b_avgTimelabelled_delay.html)
files. If you’ve configured a remote Git repository (see
?wflow_git_remote), click on the hyperlinks in the table
below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 2c1fd06 | knowlabUnimelb | 2025-07-29 | Fix markdown in 2a and update analysis code to use shared file repo in 2b |
| html | 2e6ecdf | knowlabUnimelb | 2022-11-09 | Build site. |
| Rmd | 67e1aac | knowlabUnimelb | 2022-11-09 | Publish data and analysis files |
Ruby Sternberg1, Ami Eidels2, and Daniel R. Little1
1 The University of Melbourne, 2 The University of Newcastle
Method
Participants
We tested 100 participants (80 F, 17 M, 3 Undeclared). Participants were recruited through the Melbourne School of Psychological Sciences Research Experience Pool (Mean age = 20.3298969, range = 17 - 60). Participants were reimbursed with credit toward completion of a first-year psychology subject.
were assigned to the Fixed Difficulty condition. In this condition, the location of easy, medium, hard, and very hard random dot kinematograms (RDK’s) was held constant across trials.
were assigned to the Random Difficulty condition. In this condition, the location of easy, medium, hard, and very hard random dot kinematograms (RDK’s) were randomized from trial to trial.
The Fixed Difficulty experiment was completed before the Random Difficulty experiment. Participants only completed one of these.
Design
In each condition, participants completed multiple trials in which they selected and completed RDK tasks. On each trial, participants were shown a set of four RDKs labelled by the average completion time. From the set of four RDKs, participants selected and completed one RDK at a time in any order. The goal of each trial was to complete as many as possible before a deadline. If an incorrect RDK response was made, that RDK was restarted at the same coherence but with a resampled direction (so the direction may have changed), and the participant had to respond to the RDK again. A new task could not be selected until the RDK was completed successfully.

| Version | Author | Date |
|---|---|---|
| 2e6ecdf | knowlabUnimelb | 2022-11-09 |
Participants first completed 10 trials with a long (30 sec) deadline to help participants learn the task, explore strategies, and allow for comparison to a short-deadline condition. We term this the no deadline condition since the provided time is well beyond what is necessary to complete all four RDK’s. Next, participants completed 30 trials with a 6 second deadline.
Data Cleaning
Subjects completed the experiment by clicking a link with the uniquely generated id code. Subjects were able to use the link multiple times; further, subjects were able to exit the experiment at any time. Consequently, the datafile contains partially completed data for some subjects which needed to be identified and removed.
After removing any participants who had less than chance accuracy on the easiest RDK indicating equipment problems or a misunderstanding of task directions, there were 41 and 51 in the fixed and random location conditions, respectively.
Data Analysis
We first summarize performance by answering the following questions:
Task completions
- How many tasks are completed on average?
Across both conditions, participants completed 3.91 tasks during the untimed phase and 3.44 tasks during the deadline phase.
RDK performance
We next analysed performance on the RDK discriminations. We then asked:
- What was the average completion time and accuracy of the easy, medium, hard, and very hard tasks?
RTs became shorter and more accurate as the difficulty of the RDK became easier. As expected, the RTs were shorter under a deadline than without a deadline. We visualised the response times in two ways: First, we simply took the average of each attempt on each RDK.

| Version | Author | Date |
|---|---|---|
| 2e6ecdf | knowlabUnimelb | 2022-11-09 |
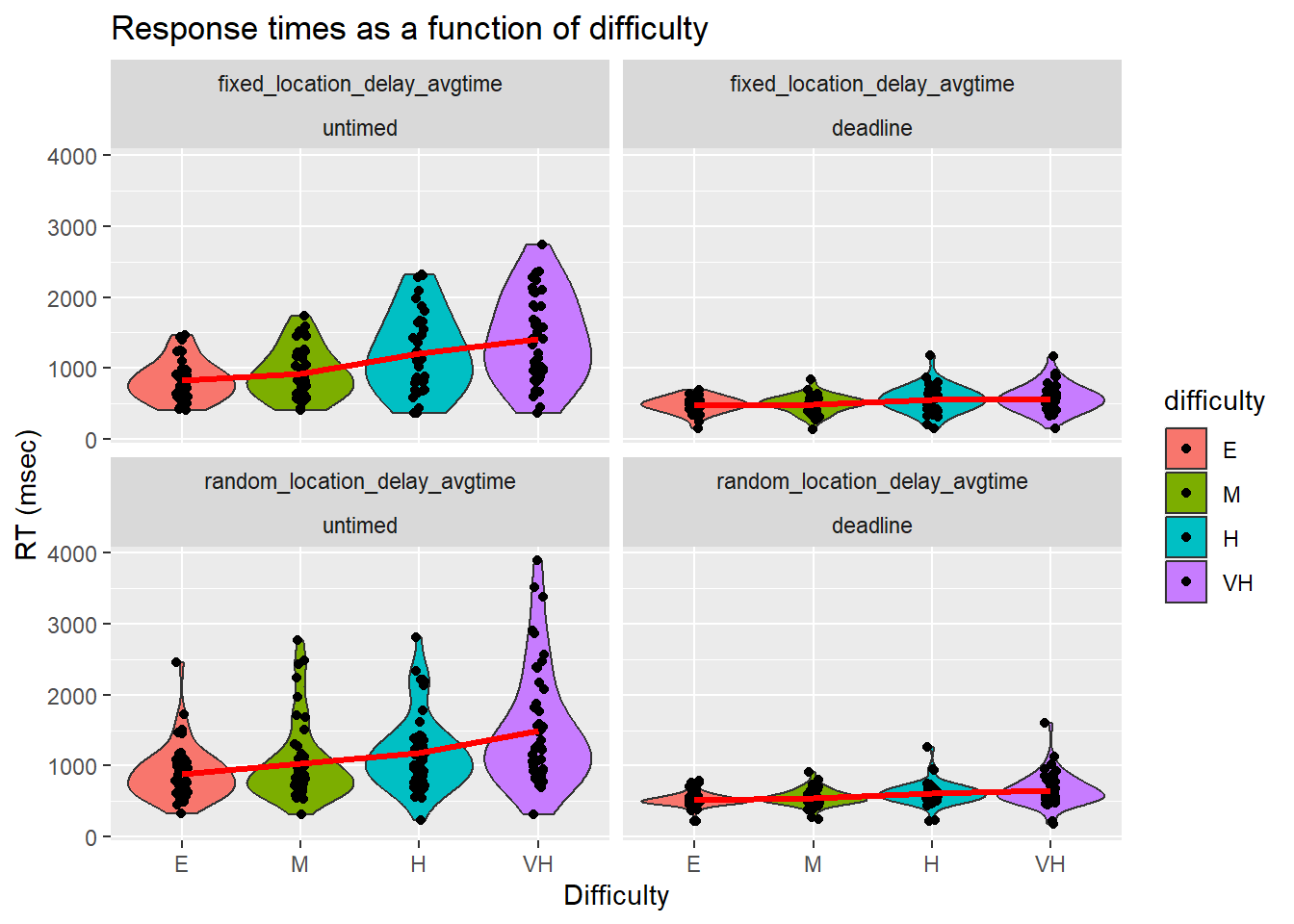
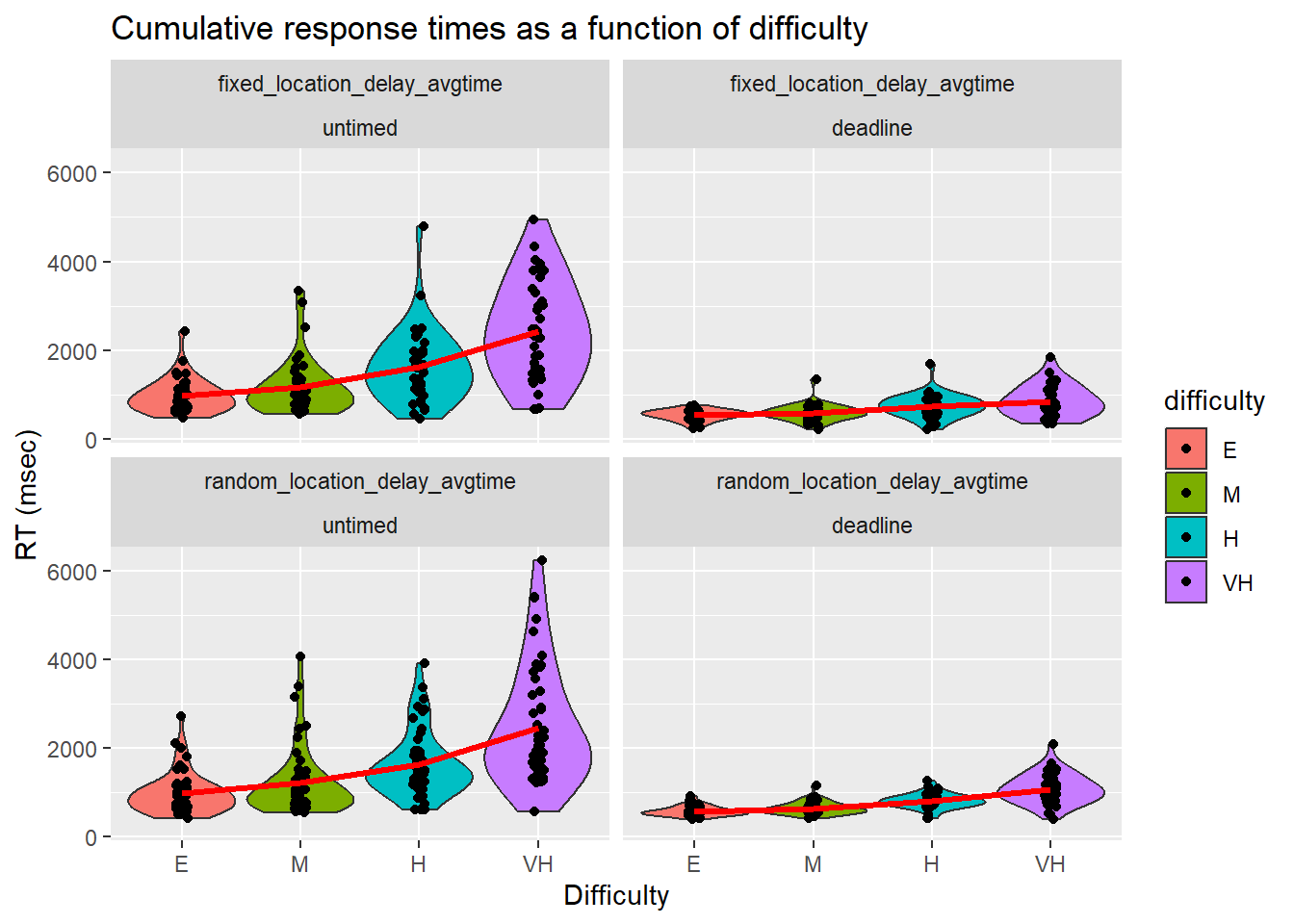
Second, we computed the time to complete an RDK as the cumulative sum across multiple attempts within a trial (termed Cumulative RT or cRT). That is, if an error is made and the RDK needs to be repeated, then the total RT is the sum of both attempts.
We further broke down RTs by condition, deadline, and difficulty.
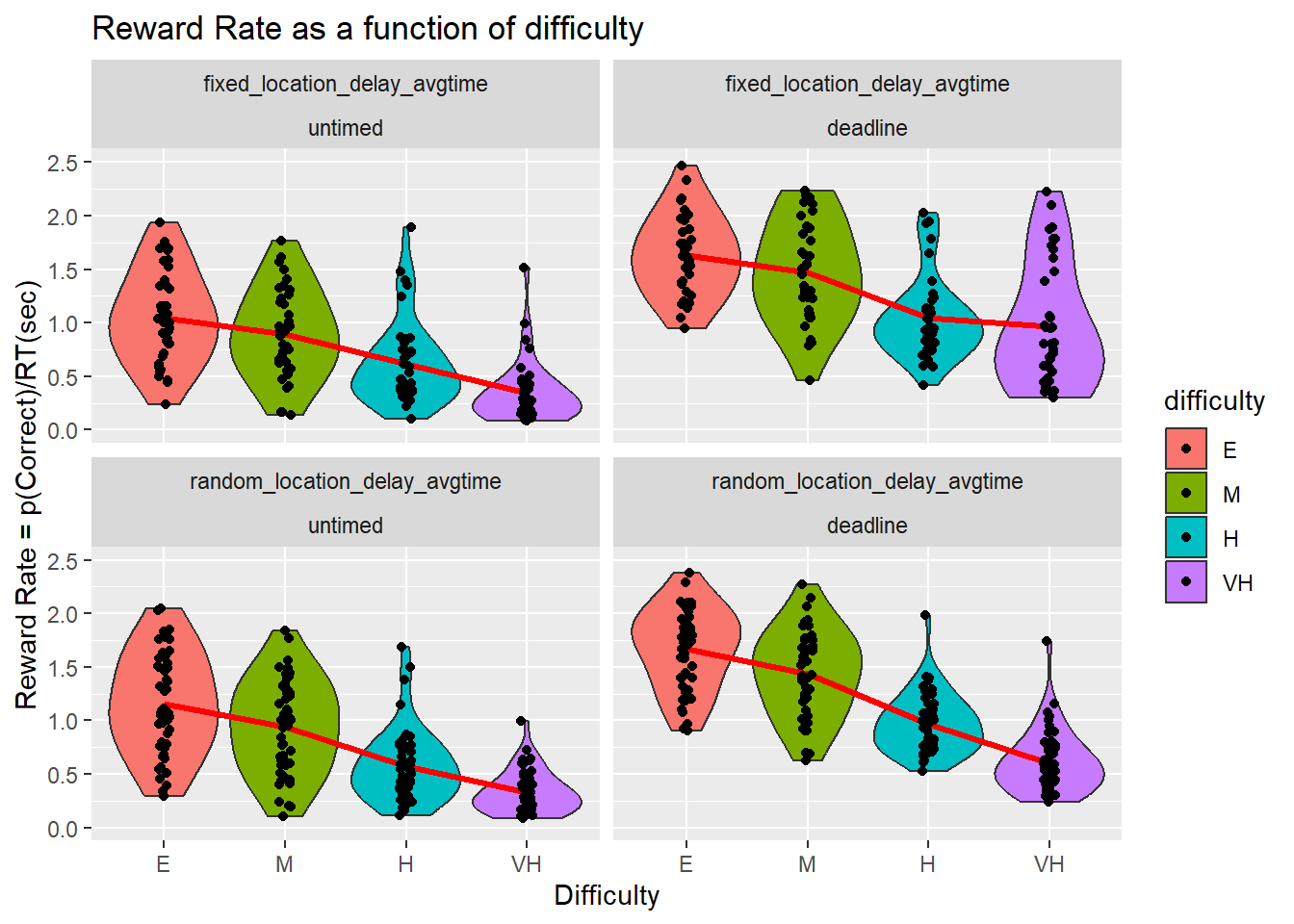
Reward Rate
| name[none] | ss[none] | df[none] | ms[none] | F[none] | p[none] | partEta[none] | |
|---|---|---|---|---|---|---|---|
| “Phase” | Phase | 58.230 | 1 | 58.230 | 145.934 | 0.000 | 0.621 |
| [“Phase”,“condition”] | Phase:condition | 4.039 | 1 | 4.039 | 10.123 | 0.002 | 0.102 |
| [“Phase”,“condition”,“.RES”] | Residual | 35.513 | 89 | 0.399 | NA | NA | NA |
| “Difficulty” | Difficulty | 78.465 | 3 | 26.155 | 232.544 | 0.000 | 0.723 |
| [“Difficulty”,“condition”] | Difficulty:condition | 0.933 | 3 | 0.311 | 2.766 | 0.042 | 0.030 |
| [“Difficulty”,“condition”,“.RES”] | Residual | 30.030 | 267 | 0.112 | NA | NA | NA |
| [“Phase”,“Difficulty”] | Phase:Difficulty | 1.045 | 3 | 0.348 | 4.883 | 0.003 | 0.052 |
| [“Phase”,“Difficulty”,“condition”] | Phase:Difficulty:condition | 0.208 | 3 | 0.069 | 0.973 | 0.406 | 0.011 |
| [“Phase”,“Difficulty”,“condition”,“.RES”] | Residual | 19.041 | 267 | 0.071 | NA | NA | NA |
| name | ss | df | ms | F | p | partEta | |
|---|---|---|---|---|---|---|---|
| “condition” | condition | 2.974 | 1 | 2.974 | 4.761 | 0.032 | 0.051 |
| “Residual” | Residual | 55.591 | 89 | 0.625 | NA | NA | NA |
Optimality in each condition
Having now established that the RDK’s are ordered in accuracy, difficulty, and reward rate, it is clear that the task set presented to each subject has an optimal solution, ordered from easiest to most difficult. We now ask:
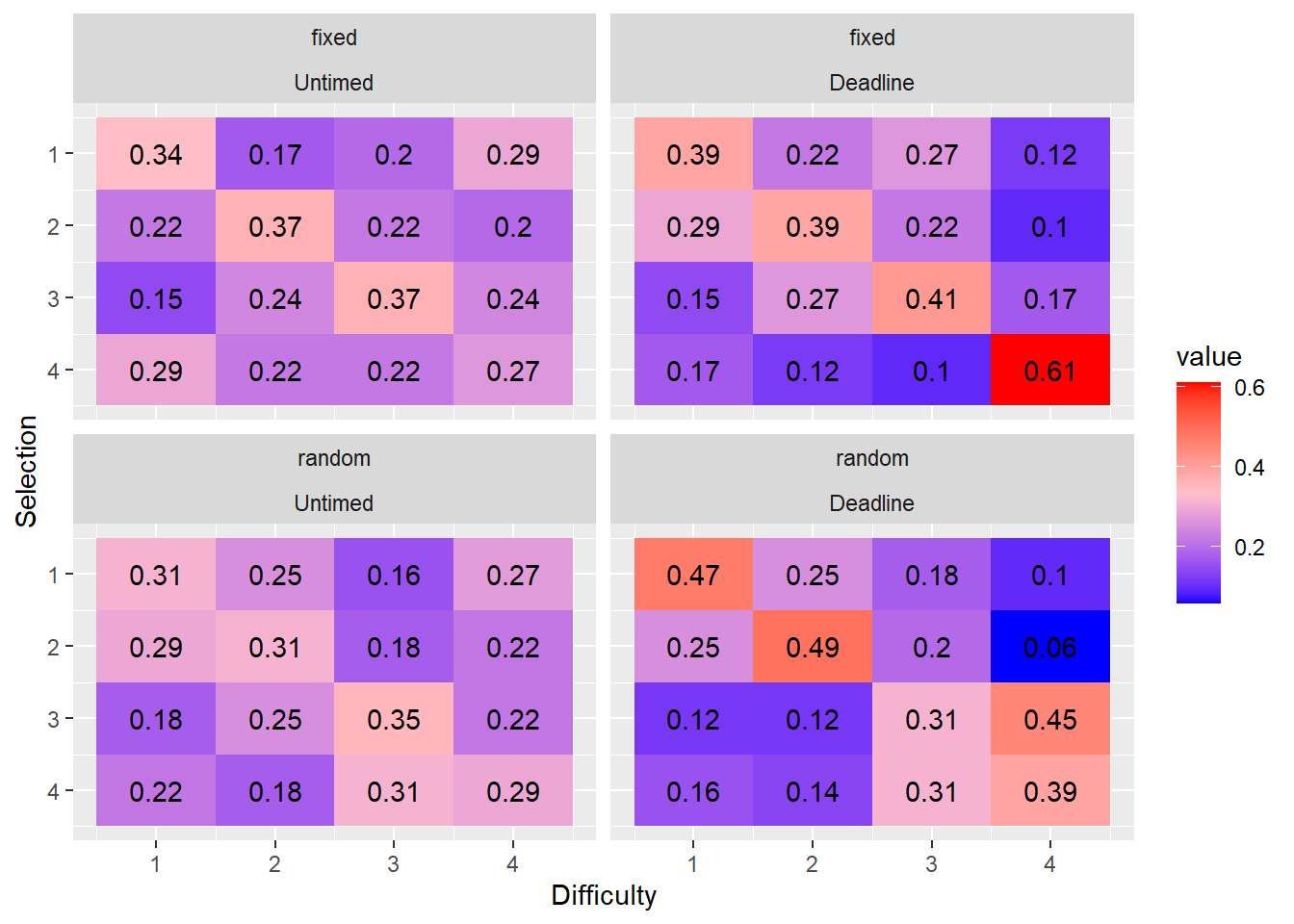
- What is the proportion of easy, medium, hard, and very hard tasks selected first, second, third or fourth?
We first compute the marginal distribution of the ranks of each of the tasks; in other words, what are the proportions of the ranks of each task in each rank position. These matrices indicate the proportions of responses for each difficulty level which were chosen first, second, third, or fourth, respectively. The matrix from a dataset in which choice is always optimal would have ones on the diagonal and zeros on the off-diagonal.
- Do the marginal distributions differ from uniformity?
We tested whether the marginal distributions were different from uniformally random selection using the fact that the mean rank is distributed according to a \(\chi^2\) distribution with the following test-statistic: \[\chi^2 = \frac{12N}{k(k+1)}\sum_{j=1}^k \left(m_j - \frac{k+1}{2} \right)^2\] see (Marden, 1995).
condition phase chi2 df p1 fixed_location_delay_avgtime untimed 0.60 3 0.23 2 fixed_location_delay_avgtime deadline 20.18 3 0.00 3 random_location_delay_avgtime untimed 5.19 3 0.07 4 random_location_delay_avgtime deadline 27.49 3 0.00 It is evident at a glance that the ordering of choices is more optimal when the locations are fixed; that is, the proportions on the diagonal are higher. When the locations are fixed, choice order becomes more optimal under a deadline. By contrast, when locations are random, responding becomes less optimal under a deadline. This likely reflects the additional costs of having to search for the appropriate task to complete. This search is minimised in the fixed location condition.
- How optimal were responses?
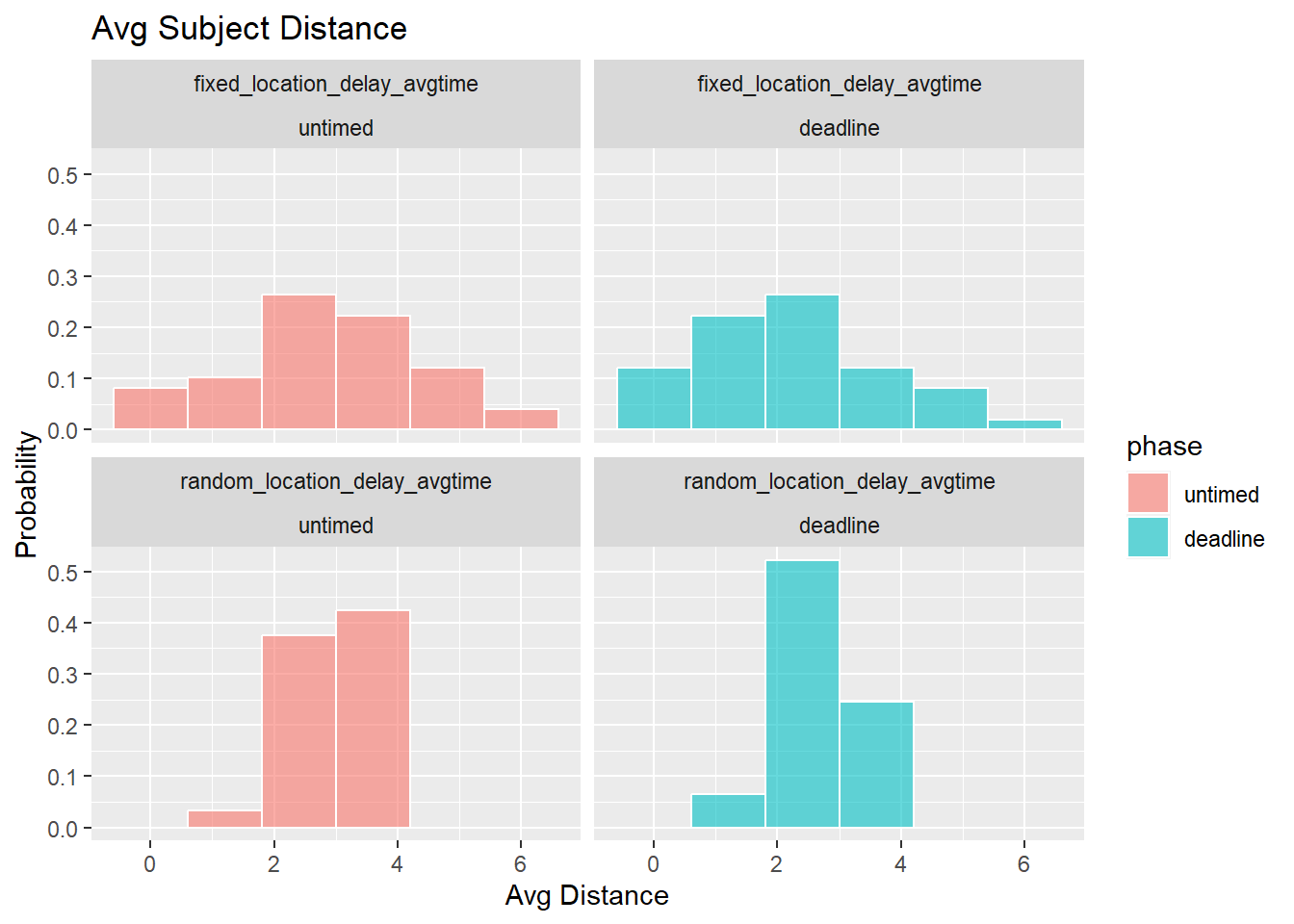
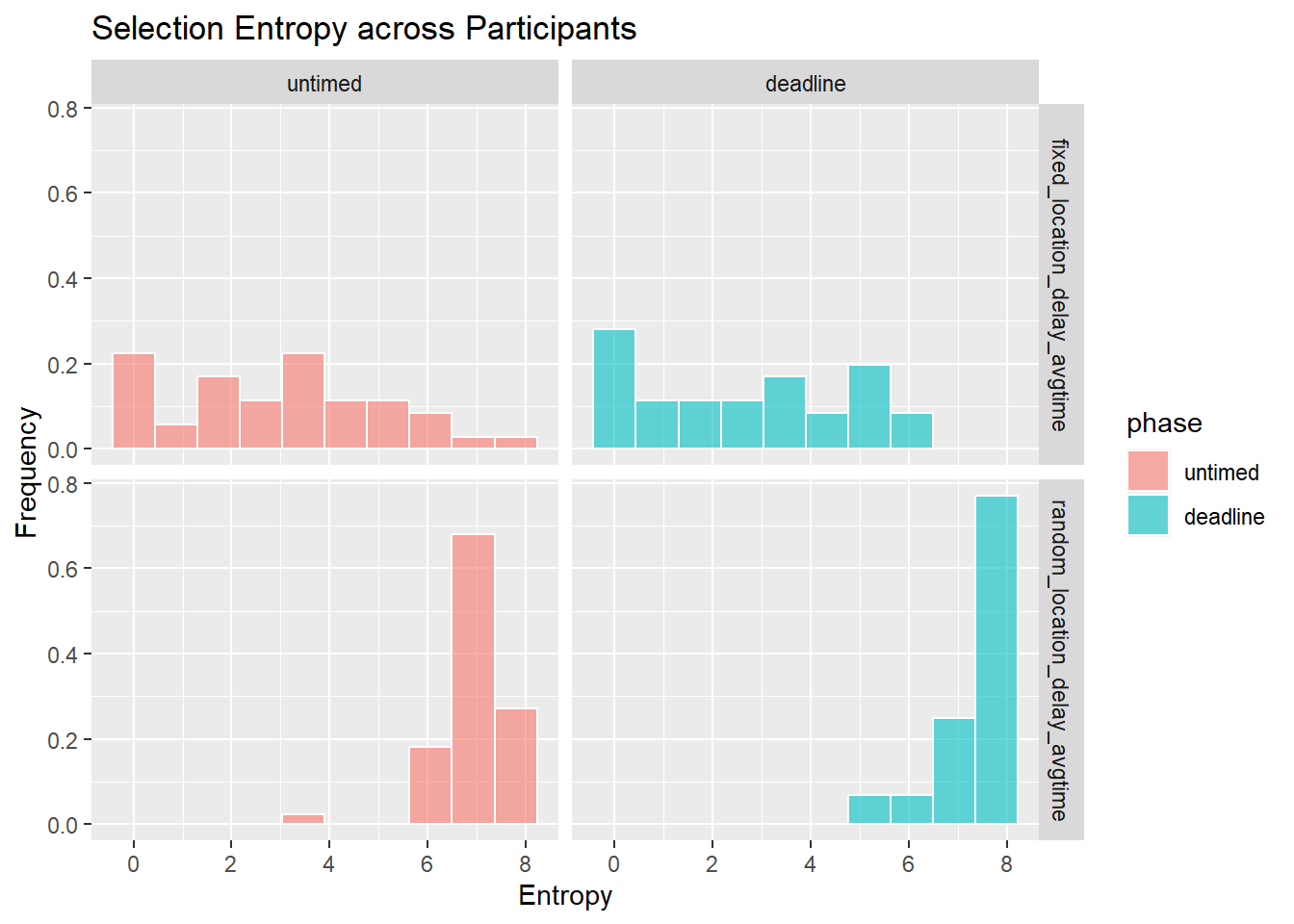
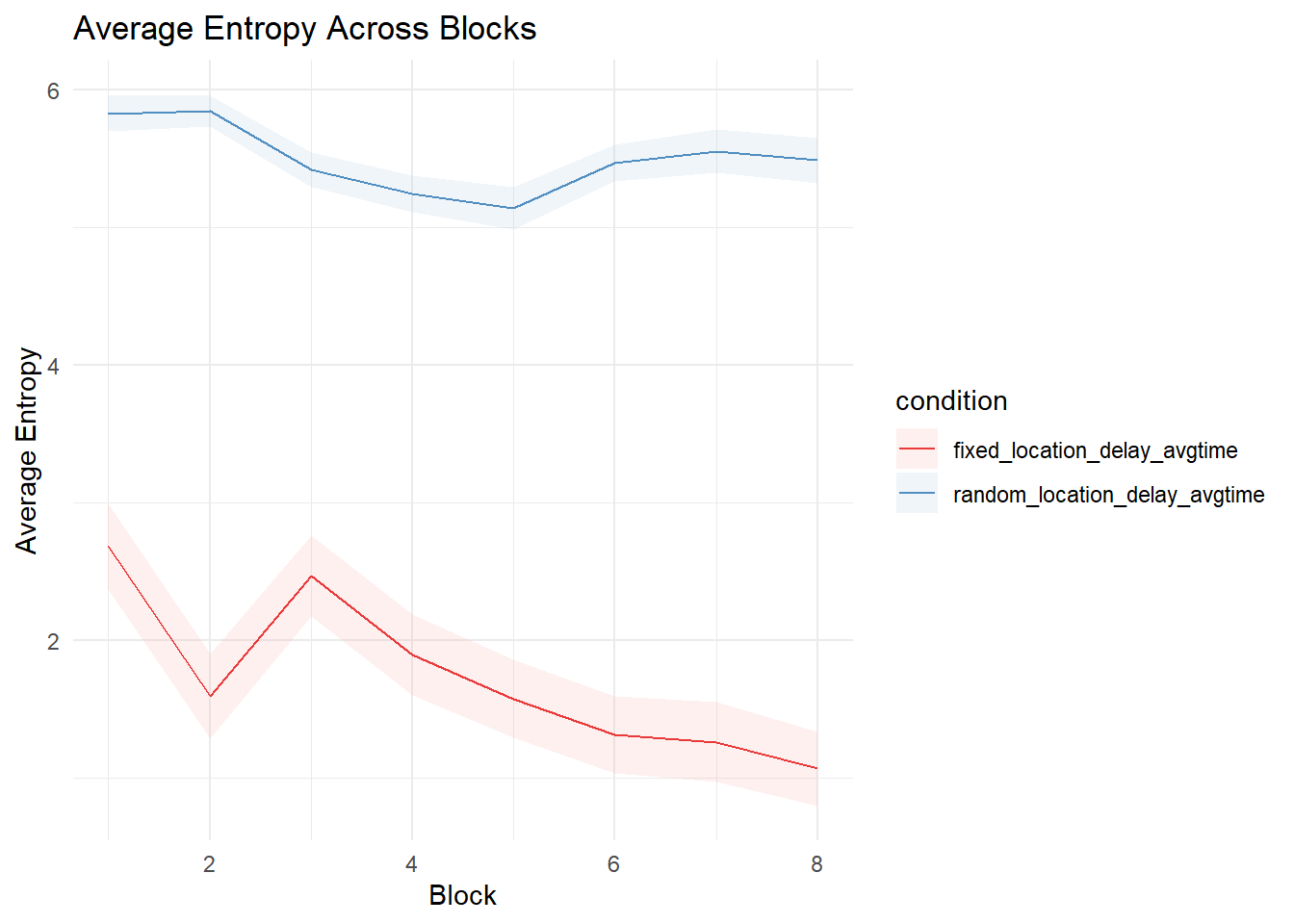
Stability of selections
Selection Choice RTs
| condition | phase | mrt_sel1 | mrt_sel2 | mrt_sel3 | mrt_sel4 |
|---|---|---|---|---|---|
| fixed_location_delay_avgtime | deadline | 663.65 | 659.36 | 641.29 | 590.01 |
| fixed_location_delay_avgtime | untimed | 1577.96 | 1290.18 | 1073.76 | 1031.92 |
| random_location_delay_avgtime | deadline | 680.02 | 669.88 | 649.91 | 596.18 |
| random_location_delay_avgtime | untimed | 1668.45 | 1248.87 | 998.97 | 962.96 |
REPEATED MEASURES ANOVA
Within Subjects Effects
───────────────────────────────────────────────────────────────────────────────────────────────────────────────
Sum of Squares df Mean Square F p η²-p
───────────────────────────────────────────────────────────────────────────────────────────────────────────────
Phase 5.572887e+7 1 5.572887e+7 341.4668515 < .0000001
0.7988148
Phase:condition 64377.81 1 64377.81 0.3944614 0.5316279 0.0045658
Residual 1.403557e+7 86 163204.34
Selection 1.078185e+7 3 3593950.57 45.9452023 < .0000001
0.3482143
Selection:condition 487719.47 3 162573.16 2.0783415 0.1035004
0.0235965
Residual 2.018142e+7 258 78222.54
Phase:Selection 9302342.28 3 3100780.76 58.8153116 < .0000001
0.4061401
Phase:Selection:condition 340072.01 3 113357.34 2.1501511 0.0943745
0.0243919
Residual 1.360192e+7 258 52720.64
───────────────────────────────────────────────────────────────────────────────────────────────────────────────
Note. Type 3 Sums of Squares
Between Subjects Effects
────────────────────────────────────────────────────────────────────────────────────────────
Sum of Squares df Mean Square F p η²-p
────────────────────────────────────────────────────────────────────────────────────────────
condition 10977.61 1 10977.61 0.02152052 0.8837132 0.0002502
Residual 4.386857e+7 86 510099.62
────────────────────────────────────────────────────────────────────────────────────────────
Note. Type 3 Sums of Squares
ASSUMPTIONS
Tests of Sphericity
───────────────────────────────────────────────────────────────────────────────────────────
Mauchly’s W p Greenhouse-Geisser ε Huynh-Feldt ε
───────────────────────────────────────────────────────────────────────────────────────────
Phase 1.0000000 NaN ᵃ 1.0000000 1.0000000
Selection 0.2101701 < .0000001 0.5263992 0.5345846
Phase:Selection 0.2846960 < .0000001 0.5621699 0.5721756
───────────────────────────────────────────────────────────────────────────────────────────
ᵃ The repeated measures has only two levels. The assumption of
sphericity is always met when the repeated measures has only two
levels.
Homogeneity of Variances Test (Levene’s)
───────────────────────────────────────────────────────── F df1 df2
p
───────────────────────────────────────────────────────── rt1_untimed
1.74125011 1 86 0.1904827
rt2_untimed 0.33645910 1 86 0.5633969
rt3_untimed 0.26473123 1 86 0.6082080
rt4_untimed 1.45923731 1 86 0.2303629
rt1_deadline 0.01961117 1 86 0.8889559
rt2_deadline 0.77861357 1 86 0.3800253
rt3_deadline 0.24419282 1 86 0.6224540
rt4_deadline 0.01164603 1 86 0.9143131
─────────────────────────────────────────────────────────
Selection model
We can treat each task selection as a probabilistic choice given by a Luce’s choice rule (Luce, 1959), where each task is represented by some strength, \(\nu\). The probability of selecting task \(i_j\) from set \(S = \{i_1, i_2, ..., i_J \}\), where J is the number of tasks, is:
\[p\left(i_j |S \right) = \frac{\nu_{i_j}}{\sum_{i \in S} \nu_{i}}. \]
Plackett (1975) generalised this model to explain the distribution over a sequence of choices (i.e., ranks). In this case, after each choice, the choice set is reduce by one (i.e., sampling without replacement). This probability of observing a specific selection order, \(i_1 \succ ... \succ i_J\) is:
\[p\left(i_j |A \right) = \prod_{j=1}^J \frac{\nu_{i_j}}{\sum_{i \in A_j} \nu_{i}}, \]
where \(A_j\) is the current choice set.
sessionInfo()R version 4.3.1 (2023-06-16 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19045)
Matrix products: default
locale:
[1] LC_COLLATE=English_Australia.utf8 LC_CTYPE=English_Australia.utf8
[3] LC_MONETARY=English_Australia.utf8 LC_NUMERIC=C
[5] LC_TIME=English_Australia.utf8
time zone: Australia/Sydney
tzcode source: internal
attached base packages:
[1] stats4 grid stats graphics grDevices utils datasets
[8] methods base
other attached packages:
[1] statmod_1.5.0 betareg_3.2-0 jmv_2.4.9 pmr_1.2.5.1
[5] jpeg_0.1-10 rstatix_0.7.2 lmerTest_3.1-3 lme4_1.1-34
[9] Matrix_1.6-1.1 png_0.1-8 reshape2_1.4.4 knitr_1.44
[13] english_1.2-6 gtools_3.9.4 DescTools_0.99.50 lubridate_1.9.3
[17] forcats_1.0.0 stringr_1.5.0 dplyr_1.1.3 purrr_1.0.2
[21] readr_2.1.4 tidyr_1.3.0 tibble_3.2.1 ggplot2_3.4.3
[25] tidyverse_2.0.0 workflowr_1.7.1
loaded via a namespace (and not attached):
[1] gld_2.6.6 sandwich_3.0-2 readxl_1.4.3
[4] rlang_1.1.1 magrittr_2.0.3 multcomp_1.4-25
[7] git2r_0.32.0 e1071_1.7-13 compiler_4.3.1
[10] flexmix_2.3-19 getPass_0.2-2 callr_3.7.3
[13] vctrs_0.6.3 pkgconfig_2.0.3 fastmap_1.1.1
[16] backports_1.4.1 labeling_0.4.3 utf8_1.2.3
[19] promises_1.2.1 rmarkdown_2.25 tzdb_0.4.0
[22] ps_1.7.5 nloptr_2.0.3 modeltools_0.2-23
[25] xfun_0.40 cachem_1.0.8 jsonlite_1.8.7
[28] later_1.3.1 afex_1.3-0 parallel_4.3.1
[31] broom_1.0.5 R6_2.5.1 RColorBrewer_1.1-3
[34] bslib_0.5.1 stringi_1.7.12 car_3.1-2
[37] boot_1.3-28.1 estimability_1.4.1 lmtest_0.9-40
[40] jquerylib_0.1.4 cellranger_1.1.0 numDeriv_2016.8-1.1
[43] Rcpp_1.0.11 zoo_1.8-12 base64enc_0.1-3
[46] nnet_7.3-19 httpuv_1.6.11 splines_4.3.1
[49] timechange_0.2.0 tidyselect_1.2.0 rstudioapi_0.15.0
[52] abind_1.4-5 yaml_2.3.7 codetools_0.2-19
[55] processx_3.8.2 lattice_0.21-8 plyr_1.8.9
[58] withr_2.5.1 coda_0.19-4 evaluate_0.22
[61] survival_3.5-5 proxy_0.4-27 pillar_1.9.0
[64] carData_3.0-5 whisker_0.4.1 generics_0.1.3
[67] rprojroot_2.0.3 hms_1.1.3 munsell_0.5.0
[70] scales_1.2.1 rootSolve_1.8.2.4 minqa_1.2.6
[73] xtable_1.8-4 jmvcore_2.4.7 class_7.3-22
[76] glue_1.6.2 emmeans_1.8.8 lmom_3.0
[79] tools_4.3.1 data.table_1.14.8 Exact_3.2
[82] fs_1.6.3 mvtnorm_1.2-3 colorspace_2.1-0
[85] nlme_3.1-162 Formula_1.2-5 cli_3.6.1
[88] fansi_1.0.4 expm_0.999-7 gtable_0.3.4
[91] sass_0.4.7 digest_0.6.33 TH.data_1.1-2
[94] farver_2.1.1 htmltools_0.5.6 lifecycle_1.0.3
[97] httr_1.4.7 MASS_7.3-60